题目内容

若直线l1：x+3y+m=0（m＞0）与直线l2：2x+6y-3=0的距离为
10
，则m=（　　）
A、7
B、
17
2
C、14
D、17
分析：直线l1即 2x+6y+2m=0，根据它与直线l2：2x+6y-3=0的距离为
10
，可得
|2m+3|
4+36
=
10
，由此求得m的值．
解答：解：直线l1：x+3y+m=0（m＞0），即 2x+6y+2m=0，
∵它与直线l2：2x+6y-3=0的距离为
10
，
∴
|2m+3|
4+36
=
10
，求得m=
17
2
，
故选：B．
点评：本题主要考查两条平行线间的距离公式的应用，要注意先把两直线的方程中x，y的系数化为相同的，然后才能用两平行线间的距离公式，属于中档题．
练习册系列答案
相关题目
已知直线l1：（2m+1）x+（m+1）y-7m-5=0（m∈R）和直线l1：x+3y-5=0，圆C：x2+y2-2x-4y=0．
（1）当m为何值时，l1∥l2？
（2）是否存在点P，使得不论m为何值，直线l1都经过点P？若存在，求出点P的坐标，若不存在，请说明理由；
（3）试判断直线l1与圆C的位置关系．若相交，求截得的弦长最短时m的值以及最短长度；若相切，求切点的坐标；若相离，求圆心到直线l1的距离的最大值．
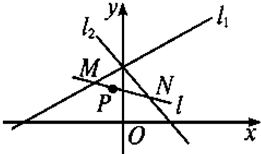如图，已知两条直线l1：x-3y+12=0，l2：3x+y-4=0，过定点P（-1，2）作一条直线l，分别与l1，l2交于M、N两点，若P点恰好是MN的中点，求直线l的方程．
（2013•西城区二模）已知直线l1：x-3y+1=0，l2：2x+my-1=0．若l1∥l2，则实数m=
-6
-6
．
已知直线l1：x-
3
y-3=0，l2：x+ty-1=0，若两直线的夹角为
π
3
，则t=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网