题目内容
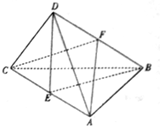 如图.在棱锥D一ABC中,若AB=CB=AD=CD=5,AC=8,BD=3
如图.在棱锥D一ABC中,若AB=CB=AD=CD=5,AC=8,BD=3 ,E,F分别是AC,BD的中点.
,E,F分别是AC,BD的中点.
(I)求证:平面DAC⊥平面ABC
(II)求三棱锥F-ABC的体积.
解:(Ⅰ)∵AB=CB=AD=CD=5,AC=8,E为AC的中点,
∴DE⊥AC,BE⊥AC,DE=BE=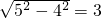 .
.
∵BD=3 ,∴DE2+BE2=18=BD2,∴DE⊥BE,
,∴DE2+BE2=18=BD2,∴DE⊥BE,
∵DE⊥BE,BE∩AC=E,
∴DE⊥平面ABC,
∵DE?平面DAC,
∴平面DAC⊥平面ABC.
(Ⅱ)∵F为BD的中点,
∴F到平面ABC的距离为 DE=
DE= .
.
∵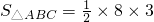 =12.
=12.
∴VF-ABC=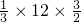 =6.
=6.
分析:(Ⅰ)由E为等腰三角形的底边AC的中点,可得DE⊥AC;在△BED中,利用勾股定理的逆定理可得DE⊥BE,从而证得结论.
(Ⅱ)由(Ⅰ)可知DE⊥平面ABC,而F点到底面ABC的距离是DE的一半,从而可计算出体积.
点评:本题考查面面垂直、三棱锥的体积,由线线垂直得到线面垂直是解决的关键.利用等腰三角形的三线合一和勾股定理的逆定理等是证垂直常用的方法.
∴DE⊥AC,BE⊥AC,DE=BE=
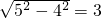 .
.∵BD=3
 ,∴DE2+BE2=18=BD2,∴DE⊥BE,
,∴DE2+BE2=18=BD2,∴DE⊥BE,∵DE⊥BE,BE∩AC=E,
∴DE⊥平面ABC,
∵DE?平面DAC,
∴平面DAC⊥平面ABC.
(Ⅱ)∵F为BD的中点,
∴F到平面ABC的距离为
 DE=
DE= .
.∵
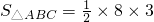 =12.
=12.∴VF-ABC=
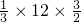 =6.
=6.分析:(Ⅰ)由E为等腰三角形的底边AC的中点,可得DE⊥AC;在△BED中,利用勾股定理的逆定理可得DE⊥BE,从而证得结论.
(Ⅱ)由(Ⅰ)可知DE⊥平面ABC,而F点到底面ABC的距离是DE的一半,从而可计算出体积.
点评:本题考查面面垂直、三棱锥的体积,由线线垂直得到线面垂直是解决的关键.利用等腰三角形的三线合一和勾股定理的逆定理等是证垂直常用的方法.

练习册系列答案
相关题目
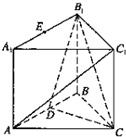 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.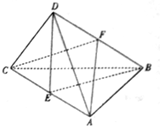 如图.在棱锥D一ABC中,若AB=CB=AD=CD=5,AC=8,BD=3
如图.在棱锥D一ABC中,若AB=CB=AD=CD=5,AC=8,BD=3
 (2013•青岛一模)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB中点,过A、N、D三点的平面交PC于M.
(2013•青岛一模)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB中点,过A、N、D三点的平面交PC于M.