题目内容
14.在△ABC中,∠A=θ,D、E分别为AB、AC的中点,且BE⊥CD,则cos2θ的最小值为$\frac{1}{8}$.分析 不妨设C(2,0),B(x,y),A(0,0),根据$\overrightarrow{BE}$•$\overrightarrow{CD}$=0,可得${(x-\frac{5}{2})}^{2}$+y2=$\frac{9}{4}$,故点B在此圆上.过点A作圆的切线,故当点B为切点时,∠A最大,即θ最大,故cosθ最小,从而求得cos2θ的最小值.
解答  解:△ABC中,∠A=θ,D、E分别为AB、AC的中点,且BE⊥CD,
解:△ABC中,∠A=θ,D、E分别为AB、AC的中点,且BE⊥CD,
如图所示,不妨设C(2,0),B(x,y),A(0,0),
∵AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,∴E(1,0),D($\frac{x}{2}$,$\frac{y}{2}$).
∵BE⊥CD,∴$\overrightarrow{BE}$•$\overrightarrow{CD}$=(1-x,-y)•($\frac{x}{2}$-2,$\frac{y}{2}$)=(1-x)($\frac{x}{2}$-2)-y•$\frac{y}{2}$=-$\frac{1}{2}$[${(x-\frac{5}{2})}^{2}$+y2-$\frac{9}{4}$]=0,
∴${(x-\frac{5}{2})}^{2}$+y2=$\frac{9}{4}$,表示以($\frac{5}{2}$,0)为圆心,半径等于$\frac{3}{2}$的圆,故点B在此圆上.
过点A作圆的切线,故当点B为切点时,∠A最大,即θ最大,故cosθ=$\frac{AB}{AC}$=$\frac{\frac{3}{2}}{2}$=$\frac{3}{4}$最小,
则cos2θ的最小值为2cos2θ-1=2×$\frac{9}{16}$-1=$\frac{1}{8}$,
故答案为:$\frac{1}{8}$.
点评 本题考查了直线与圆的位置关系、向量垂直与数量积的关系、点到直线的距离公式、同角三角函数基本关系式,考查了数形结合方法、推理能力与计算能力,属于中档题.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | (-∞,-1]∪[3,+∞) | B. | (-∞,-1]∪[2,+∞) | C. | (-∞,-3]∪[1,+∞) | D. | (-∞,-2]∪[1,+∞) |
| A. | $\overrightarrow{a}$与-λ$\overrightarrow{a}$的方向相反 | B. | |-λ$\overrightarrow{a}$|≥|$\overrightarrow{a}$| | ||
| C. | |-λ$\overrightarrow{a}$|=|λ|•$\overrightarrow{a}$ | D. | $\overrightarrow{a}$与λ2$\overrightarrow{a}$的方向相同 |
 (1)函数y=log2(x-1)的图象是由y=log2x的图象如何变化得到的?
(1)函数y=log2(x-1)的图象是由y=log2x的图象如何变化得到的?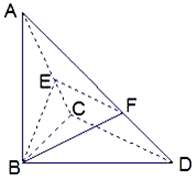 已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且$\frac{AE}{AC}=\frac{AF}{AD}$=λ(0<λ<1).
已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且$\frac{AE}{AC}=\frac{AF}{AD}$=λ(0<λ<1).