题目内容
过点(-1,1)与曲线f(x)=x3-x2-2x+1相切的直线有 条(以数字作答)
分析:设出切点坐标,求出曲线在切点处的导数,由点斜式得切线方程,代入定点坐标求切点个数得答案.
解答:解:由f(x)=x3-x2-2x+1,得f′(x)=3x2-2x-2.
设切点为(x0,x03-x02-2x0+1),
则f′(x0)=3x02-2x0-2,
∴过切点的直线方程为y-x03+x02+2x0-1=(3x02-2x0-2)(x-x0).
∵切线过点(-1,1),∴1-x03+x02+2x0-1=(3x02-2x0-2)(-1-x0),
整理得:x03+x02-x0-1=0,
解得:x0=-1或x0=1.
∴过点(-1,1)与曲线f(x)=x3-x2-2x+1相切的直线有2条.
故答案为:2.
设切点为(x0,x03-x02-2x0+1),
则f′(x0)=3x02-2x0-2,
∴过切点的直线方程为y-x03+x02+2x0-1=(3x02-2x0-2)(x-x0).
∵切线过点(-1,1),∴1-x03+x02+2x0-1=(3x02-2x0-2)(-1-x0),
整理得:x03+x02-x0-1=0,
解得:x0=-1或x0=1.
∴过点(-1,1)与曲线f(x)=x3-x2-2x+1相切的直线有2条.
故答案为:2.
点评:本题考查了利用导数研究曲线上抹点的切线方程,解答的关键是正确区分所求的是曲线上在某点处的切线方程还是过某点的切线方程,是中档题也是易错题.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,AD⊥AB,BC⊥AB,AD=3,AB=4,BC=
如图,在直角梯形ABCD中,AD⊥AB,BC⊥AB,AD=3,AB=4,BC=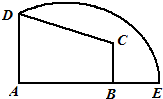 如图,在直角梯形ABCD中,AD⊥AB,BC⊥AB,AD=3,AB=4,BC=
如图,在直角梯形ABCD中,AD⊥AB,BC⊥AB,AD=3,AB=4,BC= ,点E在线段AB的延长线上.曲线段DE上任一点到A、B两点的距离之和都相等.
,点E在线段AB的延长线上.曲线段DE上任一点到A、B两点的距离之和都相等. 与A′nAn(n =1,2,3,…)交于Bn,记新的曲边梯形A′nBnBn+1A′n+1,面积为bn,求
与A′nAn(n =1,2,3,…)交于Bn,记新的曲边梯形A′nBnBn+1A′n+1,面积为bn,求 的前n项和Sn;
的前n项和Sn; 。
。 
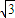 ,点E在线段AB的延长线上.曲线段DE上任一点到A、B两点的距离之和都相等.
,点E在线段AB的延长线上.曲线段DE上任一点到A、B两点的距离之和都相等.