题目内容
出以下命题其中正确的命题有______(只填正确命题的序号).
①非零向量
,
满足
⊥
,则|
+
|=|
-
|
②
•
>0,是
,
的夹角为锐角的充要条件;
③将y=lg(x-1)函数的图象按向量
=(-1,0)平移,得到的图象对应的函数为y=lgx;
④在△ABC中,若(
+
)•(
-
)=0,则△ABC为等腰三角形.
①非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
②
| a |
| b |
| a |
| b |
③将y=lg(x-1)函数的图象按向量
| a |
④在△ABC中,若(
| AB |
| AC |
| AB |
| AC |
对于①根据其几何意义,由于
⊥
,故平行四边形为矩形,又其对角线相等,故正确;对于②当共线且同向时不成立,故错误;对于③显然正确;对于④由于(
+
)•(
-
)=0,所以
2=
2,所以△ABC为等腰三角形.
故正答案为①③④
| a |
| b |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
故正答案为①③④

练习册系列答案
相关题目
 ,
, 满足
满足 +
+ )•(
)•(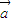 ,
,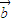 满足
满足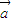 ⊥
⊥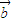 ,则|
,则|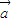 +
+ |=|
|=|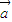 -
-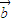 |
| •
• >0,是
>0,是 ,
, 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;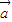 =(-1,0)平移,得到的图象对应的函数为y=lgx;
=(-1,0)平移,得到的图象对应的函数为y=lgx; +
+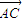 )•(
)•( -
- )=0,则△ABC为等腰三角形.
)=0,则△ABC为等腰三角形.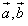 满足
满足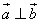 ,则
,则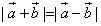 ;
;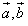 >0是
>0是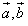 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;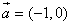 平移,得到的图像对应的函数为y=lgx;
平移,得到的图像对应的函数为y=lgx;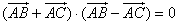 ,则△ABC为等腰三角形。
,则△ABC为等腰三角形。