题目内容
已知非零实数x,y,a,b,x,y分别为a与b,b与c的等差中项,且满足| a |
| x |
| c |
| y |
分析:欲证三个数成等比数列,只需证明中间数的平方等于前后两数之积.根据非零实数x,y,a,b,x,y分别为a与b,b与c的等差中项,把x,y用含a,b,c的式子表示,代入
+
=2,化简即可.
| a |
| x |
| c |
| y |
解答:解:证明:由x,y分别为a与b,b与c的等差中项,得x=
,y=
,
代入已知等式:
+
=2中,有
+
=2,化简整理,得b2=ac,
所以非零实数a,b,c成等比数列.
| a+b |
| 2 |
| b+c |
| 2 |
代入已知等式:
| a |
| x |
| c |
| y |
| a | ||
|
| c | ||
|
所以非零实数a,b,c成等比数列.
点评:本题考查了等比数列的证明,需要学生对等比中项的概念熟练掌握

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
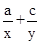 的值;
的值;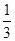 、c="-"
、c="-" 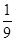 ,试计算
,试计算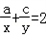 ,求证:非零实数a,b,c成等比数列.
,求证:非零实数a,b,c成等比数列.