题目内容
已知向量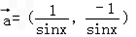
，
．
（1）若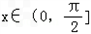
，试判断
与
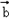能否平行？
（2）若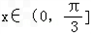
，求函数
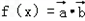的最小值．
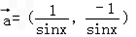，．（1）若
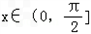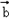，试判断与能否平行？（2）若
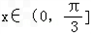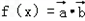，求函数的最小值．解：（1）若
与
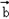平行，则有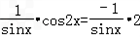
，
因为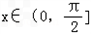
，sinx≠0，
所以得cos2x=﹣2，这与|cos2x|≤1相矛盾，
故
与
不能平行．
（2）由于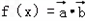
=
，
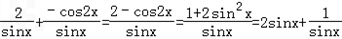又因为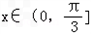
，
所以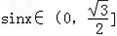
，
于是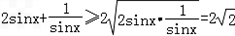
，
当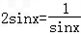
，即
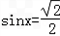时取等号．
故函数f（x）的最小值等于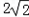
．
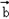与平行，则有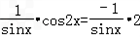，因为
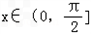，sinx≠0，所以得cos2x=﹣2，这与|cos2x|≤1相矛盾，
故
与不能平行．（2）由于
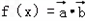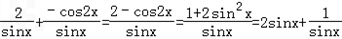=，又因为
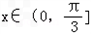，所以
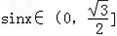，于是
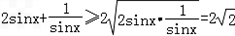，当
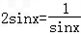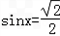，即时取等号．故函数f（x）的最小值等于
．
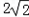练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
=
，
且
＞
，求
的范围 
+
，
，恒有
＜
，求
，
， 
⊥
, 且－
＜
＜
|
，
．
，试判断
与
能否平行？
，求函数
的最小值．
，
．
，试判断
与
能否平行？
，求函数
的最小值．
n=
.
的值；
中，角A,B,C的对边分别是a,b,c，且满足
求f(A)的取值范围.