题目内容
f(x),g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数,当x<0,f′(x)g(x)-f(x)g′(x)<0且 的解集为
的解集为
- A.(-2,0)∪(2,+∞)
- B.(-2,0)∪(0,2)
- C.(-∞,-2)∪(2,+∞)
- D.(-∞,-2)∪(0,2)
A
分析:构造函数 h(x)= ,由已知可得 x<0时,h′(x)<0,从而可得函数h(x)在(-∞,0)单调递减,又由已知可得函数 h(x)为奇函数,故可得 h(0)=g(-2)=g(2)=0,且在(0,+∞)单调递减,可求得答案.
,由已知可得 x<0时,h′(x)<0,从而可得函数h(x)在(-∞,0)单调递减,又由已知可得函数 h(x)为奇函数,故可得 h(0)=g(-2)=g(2)=0,且在(0,+∞)单调递减,可求得答案.
解答:∵f(x)和g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数
∴f(-x)=-f(x) g(-x)=g(x)
∵当x<0时,f′(x)g(x)-f(x)g′(x)<0
当x<0时, ,
,
令h(x)= ,则h(x)在(-∞,0)上单调递减
,则h(x)在(-∞,0)上单调递减
∵h(-x)=f(-x)g(-x)=-f(x)g(x)=-h(x)
∴h(x)为奇函数,
根据奇函数的性质可得函数h(x)在(0,+∞)单调递减,且h(0)=0
∵f(-2)=-f(2)=0,∴h(-2)=-h(2)=0
h(x)<0的解集为(-2,0)∪(2,+∞)
故选A.
点评:本题主要考查复合函数的求导运算和函数的单调性与其导函数正负之间的关系.导数是高考的热点问题,要多注意复习.
分析:构造函数 h(x)=
 ,由已知可得 x<0时,h′(x)<0,从而可得函数h(x)在(-∞,0)单调递减,又由已知可得函数 h(x)为奇函数,故可得 h(0)=g(-2)=g(2)=0,且在(0,+∞)单调递减,可求得答案.
,由已知可得 x<0时,h′(x)<0,从而可得函数h(x)在(-∞,0)单调递减,又由已知可得函数 h(x)为奇函数,故可得 h(0)=g(-2)=g(2)=0,且在(0,+∞)单调递减,可求得答案.解答:∵f(x)和g(x)(g(x)≠0)分别是定义在R上的奇函数和偶函数
∴f(-x)=-f(x) g(-x)=g(x)
∵当x<0时,f′(x)g(x)-f(x)g′(x)<0
当x<0时,
 ,
,令h(x)=
 ,则h(x)在(-∞,0)上单调递减
,则h(x)在(-∞,0)上单调递减∵h(-x)=f(-x)g(-x)=-f(x)g(x)=-h(x)
∴h(x)为奇函数,
根据奇函数的性质可得函数h(x)在(0,+∞)单调递减,且h(0)=0
∵f(-2)=-f(2)=0,∴h(-2)=-h(2)=0
h(x)<0的解集为(-2,0)∪(2,+∞)
故选A.
点评:本题主要考查复合函数的求导运算和函数的单调性与其导函数正负之间的关系.导数是高考的热点问题,要多注意复习.

练习册系列答案
相关题目
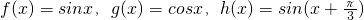 ;
;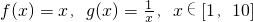 的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.
的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围. ;
; 的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.
的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.