题目内容
已知数列{an},an=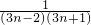 则该数前50项S50=________.
则该数前50项S50=________.
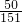
分析:可用裂项法,将an=
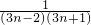 转化为:an=
转化为:an= (
( -
- ),利用累加法可求得:S50=
),利用累加法可求得:S50= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+( -
- )]的值.
)]的值.解答:∵an=
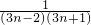 =
= (
( -
- ),
),∴S50=
 [(1-
[(1- )+(
)+( -
- )+…+(
)+…+( -
- )]
)]=
 (1-
(1- )
)=
 ×
×
=
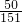 .
.故答案为:
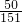 .
.点评:本题考查数列的求和,难点在于将an=
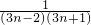 裂项为:an=
裂项为:an= (
( -
- ),再用累加法求和,属于中档题.
),再用累加法求和,属于中档题. 
练习册系列答案
相关题目