题目内容
已知
=(2,0),
=(2,2),
=(
cosα,
sinα),则
与
夹角的取值范围是( )
| OB |
| OC |
| CA |
| 2 |
| 2 |
| OA |
| OB |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
分析:向量
=
+
=(2+
cosα,2+
sinα)是一个变动的向量,其终点轨迹的参数方程是
其中α是参数,这个方程是圆的参数方程,而向量
是x轴的一个方向向量,求解的问题就转化为求
与y轴的正半轴所成的角的范围,通过数形结合求解.
| OA |
| OC |
| CA |
| 2 |
| 2 |
|
| OB |
| OA |
解答: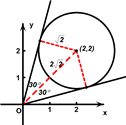 解:由
解:由
=
+
=(2+
cosα,2+
sinα),设A(x,y),则
其中α是参数,
化为普通方程即(x-2)2+(y-2)2=2,
这是一个以点(2,2)为圆心、
为半径的圆,
作出图象如图,从图中可知两向量
,
夹角的取值范围是[
,
].
故选:C.
 解:由
解:由| OA |
| OC |
| CA |
| 2 |
| 2 |
|
化为普通方程即(x-2)2+(y-2)2=2,
这是一个以点(2,2)为圆心、
| 2 |
作出图象如图,从图中可知两向量
| OA |
| OB |
| π |
| 12 |
| 5π |
| 12 |
故选:C.
点评:本题主要考查的是平面向量,但解答试题不是单独依靠平面向量的知识所能解决的,其中涉及到圆的参数方程、直线与圆的位置关系,最重要的是得具备这种在不同学科知识之间进行相互转化的思想意识,这才是本题考查的核心所在.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目