题目内容
已知点A,B的坐标分别是(0,-1),(0,1),直线AM,BM相交于点M,且它们的斜率之积- .
.(1)求点M轨迹C的方程;
(2)若过点D(2,0)的直线l与(1)中的轨迹C交于不同的两点D、F(E在D、F之间),试求△ODE与△ODF面积之比的取值范围(O为坐标原点).
【答案】分析:(1)设M(x,y),∵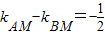 ,∴
,∴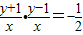 ,整理后就得到动点M的轨迹方程.
,整理后就得到动点M的轨迹方程.
(2)设l的方程为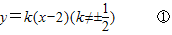 ,将①代入
,将①代入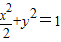 ,解得
,解得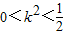 ,设E(x1,y1),F(x2,y2),则
,设E(x1,y1),F(x2,y2),则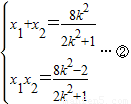 ,令λ=
,令λ=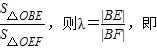
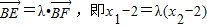 ,且0<λ<1.由此可求出△ODE与△ODF面积之比的取值范围是
,且0<λ<1.由此可求出△ODE与△ODF面积之比的取值范围是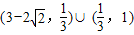 .
.
解答:解:解:(1)、设M(x,y),∵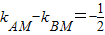 ,∴
,∴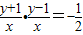 ,
,
整理得动点M的轨迹方程为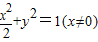 .
.
(2)由题意知直线l的斜率存在,设l的方程为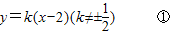
将①代入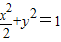 ,得l的方程为(2k2+1)x2-8k2x+(8k2-2)=0,由△>0,解得
,得l的方程为(2k2+1)x2-8k2x+(8k2-2)=0,由△>0,解得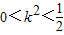 .
.
设E(x1,y1),F(x2,y2),则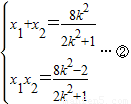
令λ=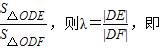
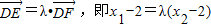 ,且0<λ<1.
,且0<λ<1.
由②得,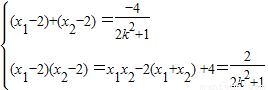 ,
,
∴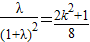 ,即
,即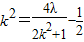
∵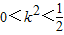 ,且
,且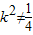 ,∴
,∴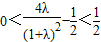 ,且
,且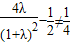 .
.
解得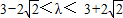 ,且
,且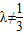 ,∵0<λ<1,∴
,∵0<λ<1,∴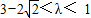 且
且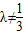 .
.
∴△OBE与△OBF面积之比的取值范围是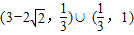 .
.
点评:本题综合考查椭圆的性质及其应用,难度较大.在解题时要认真审题,仔细解答.
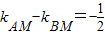 ,∴
,∴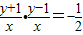 ,整理后就得到动点M的轨迹方程.
,整理后就得到动点M的轨迹方程.(2)设l的方程为
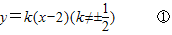 ,将①代入
,将①代入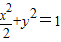 ,解得
,解得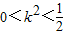 ,设E(x1,y1),F(x2,y2),则
,设E(x1,y1),F(x2,y2),则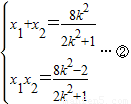 ,令λ=
,令λ=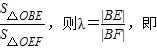
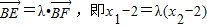 ,且0<λ<1.由此可求出△ODE与△ODF面积之比的取值范围是
,且0<λ<1.由此可求出△ODE与△ODF面积之比的取值范围是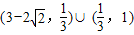 .
.解答:解:解:(1)、设M(x,y),∵
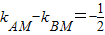 ,∴
,∴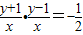 ,
,整理得动点M的轨迹方程为
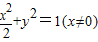 .
.(2)由题意知直线l的斜率存在,设l的方程为
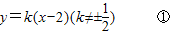
将①代入
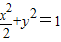 ,得l的方程为(2k2+1)x2-8k2x+(8k2-2)=0,由△>0,解得
,得l的方程为(2k2+1)x2-8k2x+(8k2-2)=0,由△>0,解得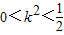 .
.设E(x1,y1),F(x2,y2),则
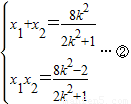
令λ=
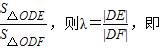
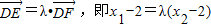 ,且0<λ<1.
,且0<λ<1.由②得,
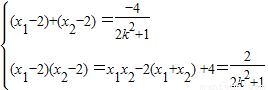 ,
,∴
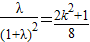 ,即
,即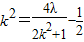
∵
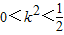 ,且
,且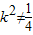 ,∴
,∴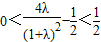 ,且
,且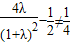 .
.解得
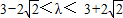 ,且
,且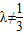 ,∵0<λ<1,∴
,∵0<λ<1,∴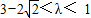 且
且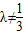 .
.∴△OBE与△OBF面积之比的取值范围是
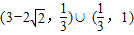 .
.点评:本题综合考查椭圆的性质及其应用,难度较大.在解题时要认真审题,仔细解答.

练习册系列答案
相关题目