题目内容

（2011•东城区一模）已知向量
a
，
b
，
c
满足
a
-
b
+2
c
=
0
，且
a
⊥
c
，|
a
|=2，|
c
|=1，则|
b
|=
2
2
2
2
．
分析：由
a
-
b
+2
c
=
0
，得
b
=
a
+2
c
  两边平方求出
b
2后再开方即可．
解答：解：∵
a
 ⊥
c
 ，∴
a
 •
c
 =0
由
a
-
b
+2
c
=
0
，得
b
=
a
+2
c
  
∴
b
2=(
a
+2
c
)2=
a
2+4
a
 •
c
 4+4
c
2=4+4×0+4×1=8
|
b
|=2
2

故答案为：2
2
．
点评：本题考查向量的基本运算、向量模的计算．属于基础题．
练习册系列答案
相关题目
（2011•东城区一模）过抛物线y2=2px（p＞0）的焦点作倾斜角为60°的直线，与抛物线分别交于A，B两点（点A在x轴上方），
|AF||BF|
=
3
3
．
（2011•东城区一模）已知α∈(
π
2
，π)，tan(α+
π
4
)=
1
7
，那么sinα+cosα的值为（　　）
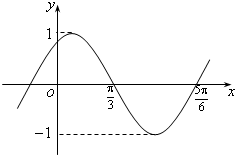（2011•东城区一模）已知函数y=sin（ωx+φ）(ω＞0， 0＜φ≤
π
2
)的部分图象如图所示，则点P（ω，φ）的坐标为（　　）
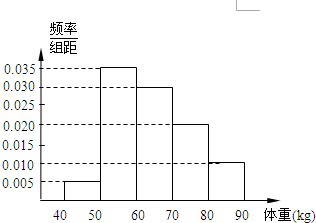（2011•东城区一模）从某地高中男生中随机抽取100名同学，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．由图中数据可知体重的平均值为
64.5
64.5
kg；若要从体重在[60，70），[70，80），[80，90]三组内的男生中，用分层抽样的方法选取12人参加一项活动，再从这12人选两人当正、负队长，则这两人身高不在同一组内的概率为
2
3
2
3
．
（2011•东城区一模）对于n∈N*（n≥2），定义一个如下数阵：Ann=
a11a12…a1n
a21a22…a2n
…………
an1an2…ann

其中对任意的1≤i≤n，1≤j≤n，当i能整除j时，aij=1；当i不能整除j时，aij=0．
（Ⅰ）当n=4时，试写出数阵A44；
（Ⅱ）设t(j)=
n
i=1
aij=a1j+a2j+…+anj．若[x]表示不超过x的最大整数，
求证：
n
j=1
t(j)=
n
i=1
[ 
n
i
 ]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网