题目内容
已知数列{an}中,a1=1,an+1(2+an)=2an(n∈N*),
(Ⅰ)求a2,a3,a4的值及数列{an}的通项公式;
(Ⅱ)记Tn=a1a2+a2a3+…+an-1an(n≥2),试判断Tn与2的大小,并说明理由.
解:(Ⅰ)由an+1(2+an)=2an(n∈N*),得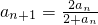 ,
,
∵a1=1,∴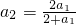 =
= ,
,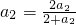 =
= ,
,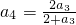 =
= . …(3分)
. …(3分)
又由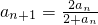 得
得 =
= +
+ ,即
,即 -
- =
= ,
,
∴{ }是以1为首项,
}是以1为首项, 为公差的等差数列,
为公差的等差数列,
∴ =1+
=1+ (n-1)=
(n-1)= ,∴
,∴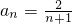 . …(7分)
. …(7分)
(Ⅱ)Tn<2. 证明如下:…(8分)
当n≥2时,an-1an= •
•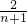 =4(
=4( ),…(10分)
),…(10分)
∴Tn=4[( )+(
)+(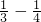 )+…+(
)+…+( )]=4(
)]=4(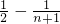 )=2-
)=2-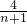 <2…(15分)
<2…(15分)
分析:(Ⅰ)由an+1(2+an)=2an(n∈N*),得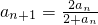 ,代入计算可求a2,a3,a4的值,确定{
,代入计算可求a2,a3,a4的值,确定{ }是以1为首项,
}是以1为首项, 为公差的等差数列,可得数列{an}的通项公式;
为公差的等差数列,可得数列{an}的通项公式;
(Ⅱ)确定数列的通项,利用裂项法求和,可判断Tn与2的大小.
点评:本题考查数列递推式,考查等差数列的证明,考查裂项法求数列的和,属于中档题.
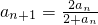 ,
,∵a1=1,∴
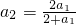 =
= ,
,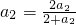 =
= ,
,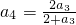 =
= . …(3分)
. …(3分)又由
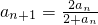 得
得 =
= +
+ ,即
,即 -
- =
= ,
,∴{
 }是以1为首项,
}是以1为首项, 为公差的等差数列,
为公差的等差数列,∴
 =1+
=1+ (n-1)=
(n-1)= ,∴
,∴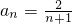 . …(7分)
. …(7分)(Ⅱ)Tn<2. 证明如下:…(8分)
当n≥2时,an-1an=
 •
•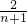 =4(
=4( ),…(10分)
),…(10分)∴Tn=4[(
 )+(
)+(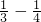 )+…+(
)+…+( )]=4(
)]=4(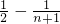 )=2-
)=2-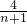 <2…(15分)
<2…(15分)分析:(Ⅰ)由an+1(2+an)=2an(n∈N*),得
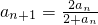 ,代入计算可求a2,a3,a4的值,确定{
,代入计算可求a2,a3,a4的值,确定{ }是以1为首项,
}是以1为首项, 为公差的等差数列,可得数列{an}的通项公式;
为公差的等差数列,可得数列{an}的通项公式;(Ⅱ)确定数列的通项,利用裂项法求和,可判断Tn与2的大小.
点评:本题考查数列递推式,考查等差数列的证明,考查裂项法求数列的和,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|