题目内容
已知 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为 .
.
(Ⅰ)如果该同学10所高校的考试都参加,试求恰有2所通过的概率;
(Ⅱ)假设该同学参加每所高校考试所需的费用均为 元,该同学决定按
元,该同学决定按 顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试,试求该同学参加考试所需费用
顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试,试求该同学参加考试所需费用 的分布列及数学期望.
的分布列及数学期望.
【答案】
本题主要考查概率与统计的基础知识,考查数据处理能力、运算求解能力以及应用用意识,考查必然与或然思想、分类与整合思想等.满分13分.
解:(Ⅰ)因为该同学通过各校考试的概率均为 ,所以该同学恰好通过2所高校自主招生考试的概率为
,所以该同学恰好通过2所高校自主招生考试的概率为
 . ………4分
. ………4分
(Ⅱ)设该同学共参加了 次考试的概率为
次考试的概率为 (
( ).
).
∵ ,
,
∴所以该同学参加考试所需费用 的分布列如下:
的分布列如下:
|
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
………7分
所以 , ………8分
, ………8分
令 , …(1)
, …(1)
则 , …(2)
, …(2)
由(1)-(2)得 ,
,
所以 , ………11分
, ………11分
所以



 (元). ………13分
(元). ………13分

练习册系列答案
相关题目










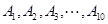 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为 .
.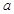 元,该同学决定按
元,该同学决定按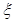 的分布列及数学期望.
的分布列及数学期望.