题目内容
已知⊙![]() 过点
过点![]() ,且与⊙
,且与⊙![]() :
:![]() 关于直线
关于直线![]() 对称.(Ⅰ)求⊙
对称.(Ⅰ)求⊙![]() 的方程;(Ⅱ)设
的方程;(Ⅱ)设![]() 为⊙
为⊙![]() 上的一个动点,求
上的一个动点,求![]() 的最小值;(Ⅲ)过点
的最小值;(Ⅲ)过点![]() 作两条相异直线分别与⊙
作两条相异直线分别与⊙![]() 相交于
相交于![]() ,且直线
,且直线![]() 和直线
和直线![]() 的倾斜角互补,
的倾斜角互补,![]() 为坐标原点,试判断直线
为坐标原点,试判断直线![]() 和
和![]() 是否平行?请说明理由.
是否平行?请说明理由.
(Ⅰ) ![]() (Ⅱ) 最小值为
(Ⅱ) 最小值为![]() (Ⅲ)略
(Ⅲ)略
解析:
解:(Ⅰ)设圆心![]()
![]() ,则
,则 ,解得
,解得![]() …………………3分
…………………3分
则圆![]() 的方程为
的方程为![]() ,将点
,将点![]() 的坐标代入得
的坐标代入得![]() ,
,
故圆![]() 的方程为
的方程为![]() …………(5分)
…………(5分)
(Ⅱ)设![]() ,则
,则![]() ,且
,且![]() …………7分
…………7分
=![]() =
=![]() ,
,
所以![]() 的最小值为
的最小值为![]() (可由线性规划或三角代换求得)…………10分
(可由线性规划或三角代换求得)…………10分
(Ⅲ)由题意知, 直线![]() 和直线
和直线![]() 的斜率存在,且互为相反数,故可设
的斜率存在,且互为相反数,故可设![]() ,
,![]() ,由
,由![]() ,
,
得![]() ……………11分
……………11分
 因为点
因为点![]() 的横坐标
的横坐标![]() 一定是该方程的解,故可得
一定是该方程的解,故可得![]() ……13分
……13分
同理,![]() ,所以
,所以![]() =
=![]()
所以,直线![]() 和
和![]() 一定平行……15分
一定平行……15分

练习册系列答案
相关题目
 过点
过点 ,且与
,且与 轴、
轴、 轴的正半轴分别交于
轴的正半轴分别交于 两点,
两点, 为坐标原点,则三角形
为坐标原点,则三角形 面积的最小值为
面积的最小值为  过点
过点 ,且与直线
,且与直线 垂直,则直线
垂直,则直线 B.
B.
 D.
D.
 过点
过点 ,且与圆
,且与圆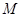 :
: 关于直线
关于直线 对称.
对称. 为圆
为圆 的最小值;
的最小值; 作两条相异直线分别与圆
作两条相异直线分别与圆 ,且直线
,且直线 和直线
和直线 的倾斜角互补,
的倾斜角互补, 为坐标原点,试判断直线
为坐标原点,试判断直线 和
和 是否平行?请说明理由.
是否平行?请说明理由. ,且与两坐标轴围成的三角形面积为5,求该直线方程。
,且与两坐标轴围成的三角形面积为5,求该直线方程。