题目内容
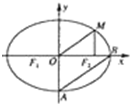 如图所示,F1、F2分别是椭圆
如图所示,F1、F2分别是椭圆 的左、右焦点,M为椭圆上一点,MF2垂直于x轴,且OM与椭圆长轴和短轴端点的连线AB平行.
的左、右焦点,M为椭圆上一点,MF2垂直于x轴,且OM与椭圆长轴和短轴端点的连线AB平行.
(1)求椭圆的离心率;
(2)过F2有与OM垂直的直线交椭圆于P、Q两点,若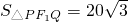 ,求椭圆的方程.
,求椭圆的方程.
解:(1)∵M为椭圆上一点,MF2垂直于x轴,∴M(c, )
)
∵OM与椭圆长轴和短轴端点的连线AB平行,
∴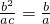
∴b=c
∴e= =
=
(2)由(1)得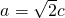 ,b=c
,b=c
联立方程组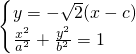 ,消元可得5y2-2
,消元可得5y2-2 cy-2c2=0
cy-2c2=0
设P(x1,y1),Q(x2,y2),则y1+y2=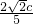 ,y1y2=-
,y1y2=-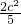
∴|y1-y2|=
∴
∴c2=b2=25,a2=50
∴椭圆的方程为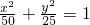
分析:(1)确定M的坐标,利用OM与椭圆长轴和短轴端点的连线AB平行,得到斜率相等,由此即可求得椭圆的离心率;
(2)由(1)得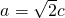 ,b=c,联立方程组
,b=c,联立方程组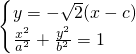 ,消元可得5y2-2
,消元可得5y2-2 cy-2c2=0,利用韦达定理,计算三角形的面积,利用已知条件即可求得椭圆的方程.
cy-2c2=0,利用韦达定理,计算三角形的面积,利用已知条件即可求得椭圆的方程.
点评:本题考查椭圆的性质,考查椭圆的标准方程,联立方程组,利用韦达定理,计算三角形的面积是关键.
 )
)∵OM与椭圆长轴和短轴端点的连线AB平行,
∴
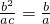
∴b=c
∴e=
 =
=
(2)由(1)得
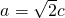 ,b=c
,b=c联立方程组
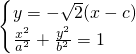 ,消元可得5y2-2
,消元可得5y2-2 cy-2c2=0
cy-2c2=0设P(x1,y1),Q(x2,y2),则y1+y2=
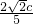 ,y1y2=-
,y1y2=-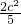
∴|y1-y2|=

∴

∴c2=b2=25,a2=50
∴椭圆的方程为
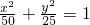
分析:(1)确定M的坐标,利用OM与椭圆长轴和短轴端点的连线AB平行,得到斜率相等,由此即可求得椭圆的离心率;
(2)由(1)得
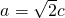 ,b=c,联立方程组
,b=c,联立方程组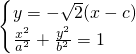 ,消元可得5y2-2
,消元可得5y2-2 cy-2c2=0,利用韦达定理,计算三角形的面积,利用已知条件即可求得椭圆的方程.
cy-2c2=0,利用韦达定理,计算三角形的面积,利用已知条件即可求得椭圆的方程.点评:本题考查椭圆的性质,考查椭圆的标准方程,联立方程组,利用韦达定理,计算三角形的面积是关键.

练习册系列答案
相关题目
 如图所示,F1,F2分别为椭圆C:
如图所示,F1,F2分别为椭圆C: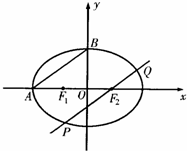 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: (2013•牡丹江一模)如图所示,F1和F2分别是双曲线
(2013•牡丹江一模)如图所示,F1和F2分别是双曲线