题目内容
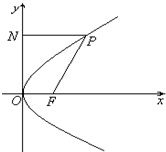
如图所示,点F(a,0)(a>0),点P在y轴上运动,M在x轴上,N为动点,且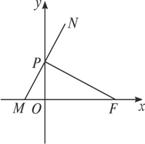
(1)求点N的轨迹C的方程;
(2)过点F(a,0)的直线l(不与x轴垂直)与曲线C交于A、B两点,设点K(-a,0),![]() 与
与![]() 的夹角为θ,求证:0<θ<
的夹角为θ,求证:0<θ<![]() .
.
解:(1)设N(x,y)、M(x0,0)、P(0,y0),
则![]() =(x0,-y0),
=(x0,-y0),![]() =(a,-y0),
=(a,-y0),![]() =(x,y-y0).
=(x,y-y0).
由![]() ·
·![]() =0,得ax0+y02=0. ①
=0,得ax0+y02=0. ①
由![]() +
+![]() =0,得(x+x0,y-2y0)=0,即
=0,得(x+x0,y-2y0)=0,即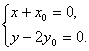 所以
所以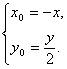
代入①,得y2=4ax即为所求.
(2)设l的方程为y=k(x-a),由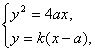 消去x,得y2-
消去x,得y2-![]() y-4a2=0.
y-4a2=0.
设A(x1,y1)、B(x2,y2),则y1y2=-4a2,![]() =(x1+a,y1),
=(x1+a,y1),![]() =(x2+a,y2),
=(x2+a,y2),
![]() ·
·![]() =(x1+a)(x2+a)+y1y2=x1x2+a(x1+x2)+a2+y1y2=
=(x1+a)(x2+a)+y1y2=x1x2+a(x1+x2)+a2+y1y2=![]() +a·(
+a·(![]() +
+![]() )+a2-4a2
)+a2-4a2
=![]() (y12+y22)-2a2>
(y12+y22)-2a2>![]() (2|y1y2|)-2a2=
(2|y1y2|)-2a2=![]() ×4a2-2a2=0,所以cosθ=
×4a2-2a2=0,所以cosθ=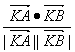 >0.所以0<θ<
>0.所以0<θ<![]() .
.

练习册系列答案
相关题目
 如图所示,点
如图所示,点 设函数f(x)定义域为(a,b),其导函数f'(x)在(a,b)内的图象如图所示,则
设函数f(x)定义域为(a,b),其导函数f'(x)在(a,b)内的图象如图所示,则 (2012•福州模拟)函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且这两点间的距离为4
(2012•福州模拟)函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且这两点间的距离为4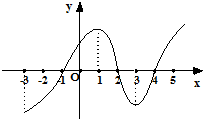 如图所示是y=f(x)的导数y=f′(x)的图象,下列四个结论:
如图所示是y=f(x)的导数y=f′(x)的图象,下列四个结论: