题目内容
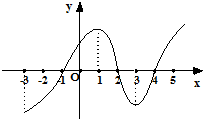如图所示是y=f（x）的导数y=f′（x）的图象，下列四个结论：①f（x）在区间（-3，1）上是增函数；
②x=-1是f（x）的极小值点；
③f（x）在区间（2，4）上是减函数，在区间（-1，2）上是增函数；
④x=2是f（x）的极小值点．
其中正确的结论是（ ）
| A、①②③ | B、②③ | C、③④ | D、①③④ |
分析：由导函数的图象可得：
利用表格即可判断出．
| x | （-3，-1） | -1 | （-1，2） | 2 | （2，4） | 4 | （4，+∞） |
| f′（x） | - | 0 | + | 0 | - | 0 | + |
| f（x） | 单减 | 极小 | 单增 | 极大 | 单减 | 极小 | 单增 |
解答：解：由导函数的图象可得：
①由表格可知：f（x）在区间（-3，1）上不具有单调性，因此不正确；
②x=-1是f（x）的极小值点，正确；
③f（x）在区间（2，4）上是减函数，在区间（-1，2）上是增函数，正确；
④x=2是f（x）的极大值点，因此不正确．
综上可知：只有②③正确．
故选：B．
| x | （-3，-1） | -1 | （-1，2） | 2 | （2，4） | 4 | （4，+∞） |
| f′（x） | - | 0 | + | 0 | - | 0 | + |
| f（x） | 单减 | 极小 | 单增 | 极大 | 单减 | 极小 | 单增 |
②x=-1是f（x）的极小值点，正确；
③f（x）在区间（2，4）上是减函数，在区间（-1，2）上是增函数，正确；
④x=2是f（x）的极大值点，因此不正确．
综上可知：只有②③正确．
故选：B．
点评：本题考查了利用导函数的图象研究函数的单调性、极值等性质，属于基础题．
练习册系列答案
相关题目
给出下列个命题：
函数y=f（x）的导函数y=f′（x）的图象如图所示，则f（x）的解析式可能是（ ）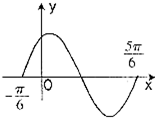
已知函数f（x）=sin（ωx+?）
