题目内容
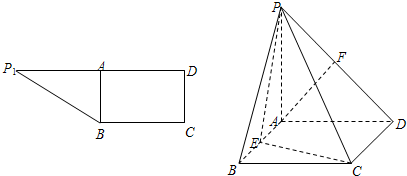
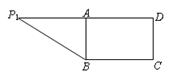
在直角梯形P1DCB中,P1D∥CB,CD∥P1D且P1D=6,BC=3,DC=
,A是P1D的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角,设E、F分别是线段AB、PD的中点.
(1)求证:AF∥平面PEC;
(2)求平面PEC和平面PAD所成的锐二面角的大小;
(3)求点D到平面PEC的距离.
| 6 |
(1)求证:AF∥平面PEC;
(2)求平面PEC和平面PAD所成的锐二面角的大小;
(3)求点D到平面PEC的距离.

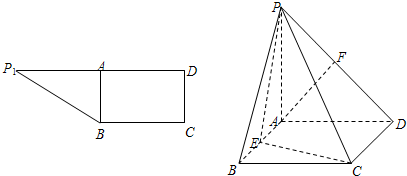
分析:(1)取PC中点M,连接FM、EM,由F、M分别为PD、PC中点,知FM=
CD,由E为AB中点,知AE=
CD,所以FM=AE,FMEA为平行四边形,由此能够证明AF∥平面PEC.
(2)延长DA,CE交于点N,连接PN,由AB⊥PA,AB⊥AD,知AB⊥平面PAD,由AB∥DC,知DC⊥平面PAD,所以∠PDA为二面角P-CD-B的平面角.由此入手能够求出平面PEC和平面PAD所成二面角.
(3)连接ED,由PA⊥平面ABCD,知VP-CED=
S△CED•PA=
,VP-CED=VD-PCE=
.由此能求出点D到平面PEC的距离.
| 1 |
| 2 |
| 1 |
| 2 |
(2)延长DA,CE交于点N,连接PN,由AB⊥PA,AB⊥AD,知AB⊥平面PAD,由AB∥DC,知DC⊥平面PAD,所以∠PDA为二面角P-CD-B的平面角.由此入手能够求出平面PEC和平面PAD所成二面角.
(3)连接ED,由PA⊥平面ABCD,知VP-CED=
| 1 |
| 3 |
| 3 |
| 2 |
| 6 |
| 3 |
| 2 |
| 6 |
解答: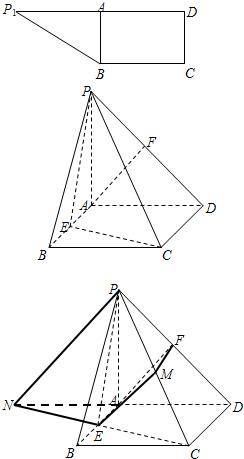 (1)证明:取PC中点M,连接FM、EM,
(1)证明:取PC中点M,连接FM、EM,
∵F、M分别为PD、PC中点,
∴FM=
CD,
∵E为AB中点,∴AE=
CD,
∴FM=AE,∴FMEA为平行四边形,
∴AF∥EM,
∵AF?平面PEC,EM?平面PEC,
∴AF∥平面PEC.
(2)解:延长DA,CE交于点N,连接PN,
∵AB⊥PA,AB⊥AD,
∴AB⊥平面PAD∵AB∥DC,…6分
∴DC⊥平面PAD,
∴DC⊥PD,DC⊥AD,
∴∠PDA为二面角P-CD-B的平面角
∴∠PDA=45°,
∵PA=AD=3∠PDA=45°,
∵PD=3
,∴PA⊥AD,
又 PA⊥AB,∴PA⊥平面ABCD,
∵AE∥CD,且E为AB中点,
∴AE=
CD,∴AE为△NDC的中位线,
∴AN=AD=PA,∴△PND为直角三角形,
又NE=EC=
,PE=
,
∴△PNC为直角三角形,
∴PC⊥PN,PD⊥PN,
∴∠CPD为平面PEC和平面PAD所成二面角的平面角,
又PD=3
,CD=
,PD⊥DC,
∴tan∠CPD=
=
=
.
∴∠CPD=30°,
∴平面PEC和平面PAD所成二面角为30°.
(3)解:连接ED,
∵PA⊥平面ABCD,
∴VP-CED=
S△CED•PA=
×
×
×3×3=
,
VP-CED=VD-PCE=
,
设点D到平面PCE的距离为d.
S△PCE=3
,
VP-PCE=
S△DCE•d=
,
∴d=
,
点D到平面PEC的距离为
.
 (1)证明:取PC中点M,连接FM、EM,
(1)证明:取PC中点M,连接FM、EM,∵F、M分别为PD、PC中点,
∴FM=
| 1 |
| 2 |
∵E为AB中点,∴AE=
| 1 |
| 2 |
∴FM=AE,∴FMEA为平行四边形,
∴AF∥EM,
∵AF?平面PEC,EM?平面PEC,
∴AF∥平面PEC.
(2)解:延长DA,CE交于点N,连接PN,
∵AB⊥PA,AB⊥AD,
∴AB⊥平面PAD∵AB∥DC,…6分
∴DC⊥平面PAD,
∴DC⊥PD,DC⊥AD,
∴∠PDA为二面角P-CD-B的平面角
∴∠PDA=45°,
∵PA=AD=3∠PDA=45°,
∵PD=3
| 2 |
又 PA⊥AB,∴PA⊥平面ABCD,
∵AE∥CD,且E为AB中点,
∴AE=
| 1 |
| 2 |
∴AN=AD=PA,∴△PND为直角三角形,
又NE=EC=
| ||
| 2 |
| ||
| 2 |
∴△PNC为直角三角形,
∴PC⊥PN,PD⊥PN,
∴∠CPD为平面PEC和平面PAD所成二面角的平面角,
又PD=3
| 2 |
| 6 |
∴tan∠CPD=
| CD |
| PD |
| ||
3
|
| ||
| 3 |
∴∠CPD=30°,
∴平面PEC和平面PAD所成二面角为30°.
(3)解:连接ED,
∵PA⊥平面ABCD,
∴VP-CED=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 6 |
| 3 |
| 2 |
| 6 |
VP-CED=VD-PCE=
| 3 |
| 2 |
| 6 |
设点D到平面PCE的距离为d.
S△PCE=3
| 3 |
VP-PCE=
| 1 |
| 3 |
| 3 |
| 2 |
| 6 |
∴d=
3
| ||
| 2 |
点D到平面PEC的距离为
3
| ||
| 2 |
点评:本题考查证明AF∥平面PEC,求平面PEC和平面PAD所成的锐二面角的大小,求点D到平面PEC的距离.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目


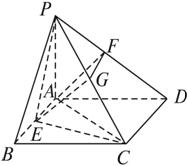
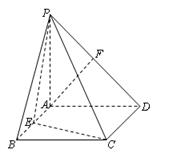
 ,A是P1D的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角,设E、F分别是线段AB、PD的中点.
,A是P1D的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角,设E、F分别是线段AB、PD的中点.