Question

如图,河宽OB=1千米,相距4千米(直线距离)的两座城市A、B分别位于河的两岸,现需铺设一条电缆连通A与B,已知地下电缆的修建费为每千米2万元,水下电缆的修建费为每千米4万元.假定两岸是平行的直线,问应如何铺设电缆可使总的修建费用最少?

(=3.873,=1.732,精确到百米、百元)

Answer 1

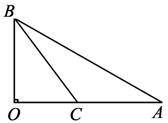
分析：这道题的背景是建设电缆工程的设计.解题关键在于确定C点的位置,由建立修建费用S的解析式所选择的不同参数可得不同的解法.

解法一：设OC=x(0≤x≤),则

AC=-x,BC=.

    总修建费S=2(-x)+4

=2+3(-x)+(+x)

=2++(+x)

≥2+2.

    当且仅当x=时,S取最小值2+2.此时,AC≈3.3,BC≈1.2,故当先铺设3.3千米地下电缆,再铺设1.2千米水下电缆连通A与B时,总的修建费用最小.此时,修建费为11.21万元.