Question

函数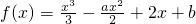在区间[-1，2]上不单调，则a的取值范围为________．

Answer 1

分析：将函数在区间上不单调，转化为函数在区间上有极值，求出导函数，令导函数的等于0在区间上有解，分离出a，求出a的范围．
解答：若函数在区间[-1，2]上不单调
则函数在[-1，2]上有极值
f′（x）=x²-ax+2
所以x²-ax+2=0在区间（-1，2）上有根，
即在区间（-1，2）上有解当2＞x＞0时，a≥，又当a=2时，f′（x）=x²-ax+2≥0，所以a＞，
当-1≤x＜0，a＜-3
所以a＜-3或a＞
所以a的取值范围为．
故答案为：．
点评：解决函数在某区间上的不单调性问题，常将其转化为熟悉的极值问题，然后利用导数来解决．