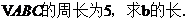题目内容
已知
(I)求 的值;
的值;
(II)求证: 与
与 互相垂直;
互相垂直;
(III)设 且k≠0,求β-α的值.
且k≠0,求β-α的值.
解:(I)解:∵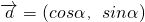 ,
,
∴ .(3分)
.(3分)
(II)证明:∵( )•(
)•( )
)
=(cosα+cosβ)(cosα-cosβ)+(sinα+sinβ)(sinα-sinβ)(6分)
=cos2α-cos2β+sin2α-sin2β
=0,
∴( )⊥(
)⊥( ).(8分)
).(8分)
(III)解:∵ ,
,
∴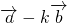 =(cosα-kcosβ,sinα-ksinβ),(10分)
=(cosα-kcosβ,sinα-ksinβ),(10分)
∴
= ,(12分)
,(12分)

= ,
,
∵|k +
+ |=|
|=| -k
-k |,
|,
∴ ,
,
整理,得2kcos(β-α)=-2kcos(β-α)
又k≠0,∴cos(β-α)=0
∵0<α<β<π,
∴0<β-α<π,
∴ .(14分)
.(14分)
分析:(I)由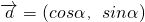 ,能求出
,能求出 的值.
的值.
(II)由( )•(
)•( )=(cosα+cosβ)(cosα-cosβ)+(sinα+sinβ)(sinα-sinβ)=0,能证明(
)=(cosα+cosβ)(cosα-cosβ)+(sinα+sinβ)(sinα-sinβ)=0,能证明( )⊥(
)⊥( ).
).
(III)由 ,
,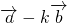 =(cosα-kcosβ,sinα-ksinβ)和|k
=(cosα-kcosβ,sinα-ksinβ)和|k +
+ |=|
|=| -k
-k |,能够求出
|,能够求出 .
.
点评:本题考查向量的模的求法,求证: 与
与 互相垂直和求β-α的值.综合性强,较繁琐,容易出错.解题时要认真审题,注意三角函数恒等变换的灵活运用.
互相垂直和求β-α的值.综合性强,较繁琐,容易出错.解题时要认真审题,注意三角函数恒等变换的灵活运用.
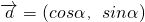 ,
,∴
 .(3分)
.(3分)(II)证明:∵(
 )•(
)•( )
)=(cosα+cosβ)(cosα-cosβ)+(sinα+sinβ)(sinα-sinβ)(6分)
=cos2α-cos2β+sin2α-sin2β
=0,
∴(
 )⊥(
)⊥( ).(8分)
).(8分)(III)解:∵
 ,
,∴
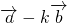 =(cosα-kcosβ,sinα-ksinβ),(10分)
=(cosα-kcosβ,sinα-ksinβ),(10分)∴

=
 ,(12分)
,(12分)
=
 ,
,∵|k
 +
+ |=|
|=| -k
-k |,
|,∴
 ,
,整理,得2kcos(β-α)=-2kcos(β-α)
又k≠0,∴cos(β-α)=0
∵0<α<β<π,
∴0<β-α<π,
∴
 .(14分)
.(14分)分析:(I)由
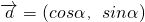 ,能求出
,能求出 的值.
的值.(II)由(
 )•(
)•( )=(cosα+cosβ)(cosα-cosβ)+(sinα+sinβ)(sinα-sinβ)=0,能证明(
)=(cosα+cosβ)(cosα-cosβ)+(sinα+sinβ)(sinα-sinβ)=0,能证明( )⊥(
)⊥( ).
).(III)由
 ,
,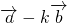 =(cosα-kcosβ,sinα-ksinβ)和|k
=(cosα-kcosβ,sinα-ksinβ)和|k +
+ |=|
|=| -k
-k |,能够求出
|,能够求出 .
.点评:本题考查向量的模的求法,求证:
 与
与 互相垂直和求β-α的值.综合性强,较繁琐,容易出错.解题时要认真审题,注意三角函数恒等变换的灵活运用.
互相垂直和求β-α的值.综合性强,较繁琐,容易出错.解题时要认真审题,注意三角函数恒等变换的灵活运用. 
练习册系列答案
相关题目
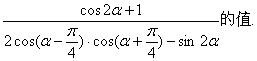

 的值;
的值;
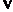 ABC中,内角A,B,C的对边分别为a,b,c.已知
ABC中,内角A,B,C的对边分别为a,b,c.已知 .
.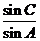 的值;
的值;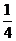 ,
,