题目内容
(本小题满分12分)在数列 中,
中, ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有 .
.
(1)证明数列 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;
(2)设数列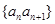 的前n项和为
的前n项和为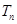 ,求使得
,求使得 的最小正整数
的最小正整数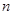 .
.
 中,
中, ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有 .
.(1)证明数列
 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;(2)设数列
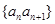 的前n项和为
的前n项和为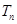 ,求使得
,求使得 的最小正整数
的最小正整数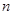 .
.(1)  (2) 91
(2) 91
 (2) 91
(2) 91试题分析:解:(1)
 ,因为
,因为 ,所以
,所以 ,
,∴ 数列
 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列,∴
 ,从而
,从而 ………… ……………………………6分
………… ……………………………6分(2) 因为

所以


 ,
, 由
 ,
,得
 ,
,最小正整数
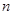 为91.………………………………………………12分
为91.………………………………………………12分点评:对于已知等差数列和等比数列的通项公式的求解,主要是求解两个基本元素,解方程组得到结论。而对于一般的数列求和思想,主要是分析其通项公式的特点,选择是用错位相减法还是裂项法,还是倒序相加法等等的求和方法来得到。属于中档题。

练习册系列答案
相关题目
 成等比数列,则
成等比数列,则 ( )
( )



 是等差数列,
是等差数列, 若
若 ,则
,则 的值是( )
的值是( )

 为等比数列,
为等比数列, 为其前
为其前 项和,已知
项和,已知 ,则公比
,则公比



 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列 项和.已知
项和.已知 ,且
,且 构成等差数列.
构成等差数列. 求数列
求数列 的前
的前 .
. 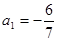 ,
,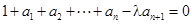 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),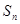 为数列{an}的前
为数列{an}的前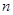 项和.
项和.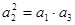 ,求
,求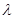 的值;
的值; ;
;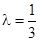 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由. 的前
的前 项和为
项和为 ,
, ,若数列
,若数列 是公比为
是公比为 的等比数列.
的等比数列.  ;
; ,
, ,求数列
,求数列 的前
的前 .
. 中,
中, 成等差数列,则
成等差数列,则 ( )
( ) 或3
或3 的公比
的公比 ,前
,前 项和为
项和为 ,则
,则 .
.