题目内容
已知函数![]() (m为实数).
(m为实数).
(1)当m=3时,解不等式 -7≤ f(x) ≤-1;
(2)若关于x的不等式 -1≤ f(x) ≤2仅有一解,求实数m的值;
(3)是否存在整数a , b,使不等式![]() 的解集恰好为[a,b],若存在,求出a,b的值;若不存在,请说明理由.
的解集恰好为[a,b],若存在,求出a,b的值;若不存在,请说明理由.
解:(1)当m=3时,![]() ,不等式 -7≤
,不等式 -7≤![]() ≤-1,等价于
≤-1,等价于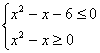 ,
,
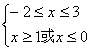 ,解得
,解得![]() 或
或![]() .……………4分
.……………4分
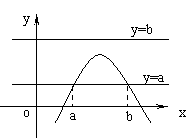
 (2)数形结合,由图象知,要使不等式组仅有1解,
(2)数形结合,由图象知,要使不等式组仅有1解,
需抛物线仅有一个点落在直线y=-1与y=2之间围成的区域内,
故抛物线只能与直线y=-1相切,所以f(x)=-1,
即![]() ,
,
由![]()
 解得m=4 . …………………………8分
解得m=4 . …………………………8分
(3)假设存在整数a , b,使不等式![]() 的解集恰好为[a,b],
的解集恰好为[a,b],
由图象可知 ,即
,即
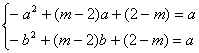 ,两式相减可得
,两式相减可得
![]() ,化简有m-2=a+b. 代入得 b(a-1)=2a .
,化简有m-2=a+b. 代入得 b(a-1)=2a .
当a=1时,等式不成立;
当a![]() 1时,有
1时,有![]() ,所以
,所以![]() ,
,
解得![]() ,
,![]() ,
,![]() ,
,
经检验![]() 或
或![]() 符合题意,
符合题意,
所以存在整数a , b,使不等式![]() 的解集恰好为[a,b]. ……………………16分
的解集恰好为[a,b]. ……………………16分

练习册系列答案
相关题目
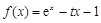 (e为自然对数的底数).
(e为自然对数的底数).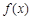 的单调增区间;
的单调增区间;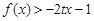 的解集为M,且集合
的解集为M,且集合 ,求实数t的取值范围.
,求实数t的取值范围. 的定义域为R,求实数m的取值范围
的定义域为R,求实数m的取值范围