题目内容
在△ABC中,已知sin(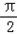 +B)=
+B)=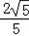 .
.
(1)求tan2B的值;
(2)若cosA=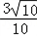 ,c=10,求△ABC的面积;
,c=10,求△ABC的面积;
(3)若函数f(x)=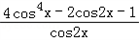 ,求f(C)+sin2C的值.
,求f(C)+sin2C的值.
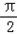 +B)=
+B)=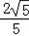 .
.(1)求tan2B的值;
(2)若cosA=
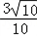 ,c=10,求△ABC的面积;
,c=10,求△ABC的面积;(3)若函数f(x)=
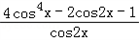 ,求f(C)+sin2C的值.
,求f(C)+sin2C的值.解:(1)∵sin(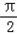 +B)=cosB=
+B)=cosB=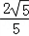 ,
,
又B为三角形的内角,
∴sinB=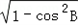 =
=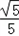 ,
,
∴tanB=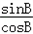 =
= ,
,
则tan2B=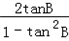 =
=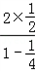 =
= ;
;
(2)∵cosA=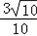 ,A为三角形的内角,
,A为三角形的内角,
∴sinA=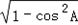 =
=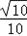 ,
,
∴sinC=sin(A+B)=sinAcosB+cosAsinB=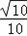 ×
×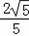 +
+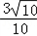 ×
×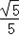 =
=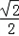 ,
,
又c=10,
∴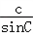 =
=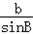 =
=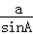 ,
,
即b=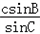 =2
=2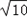 ,a=
,a=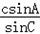 =2
=2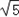 ,
,
则△ABC的面积S= bcsinA=
bcsinA= ×2
×2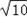 ×10×
×10×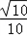 =10;
=10;
(3)∵f(x)=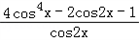 =
=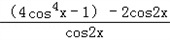 =
=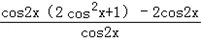 =2cos2x+1﹣2=2cos2x﹣1=cos2x,
=2cos2x+1﹣2=2cos2x﹣1=cos2x,
∴f(C)=cos2C,又a=2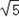 ,b=2
,b=2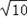 ,c=10,
,c=10,
∴cosC=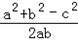 =
=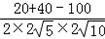 =﹣
=﹣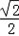 ,
,
又C为三角形的内角,
∴C=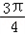 ,
,
则f(C)+sin2C=cos2C+sin2C=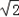 sin(2C+
sin(2C+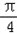 )=
)=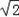 sin
sin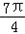 =﹣1.
=﹣1.
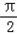 +B)=cosB=
+B)=cosB=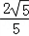 ,
,又B为三角形的内角,
∴sinB=
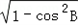 =
=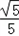 ,
,∴tanB=
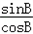 =
= ,
,则tan2B=
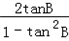 =
=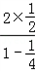 =
= ;
;(2)∵cosA=
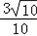 ,A为三角形的内角,
,A为三角形的内角,∴sinA=
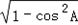 =
=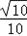 ,
,∴sinC=sin(A+B)=sinAcosB+cosAsinB=
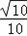 ×
×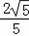 +
+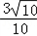 ×
×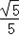 =
=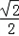 ,
,又c=10,
∴
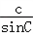 =
=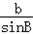 =
=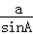 ,
,即b=
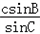 =2
=2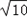 ,a=
,a=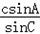 =2
=2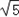 ,
,则△ABC的面积S=
 bcsinA=
bcsinA= ×2
×2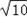 ×10×
×10×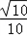 =10;
=10;(3)∵f(x)=
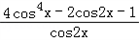 =
=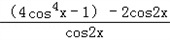 =
=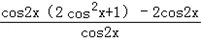 =2cos2x+1﹣2=2cos2x﹣1=cos2x,
=2cos2x+1﹣2=2cos2x﹣1=cos2x,∴f(C)=cos2C,又a=2
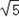 ,b=2
,b=2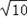 ,c=10,
,c=10,∴cosC=
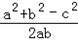 =
=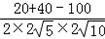 =﹣
=﹣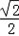 ,
,又C为三角形的内角,
∴C=
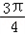 ,
,则f(C)+sin2C=cos2C+sin2C=
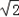 sin(2C+
sin(2C+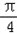 )=
)=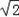 sin
sin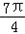 =﹣1.
=﹣1.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,已知|
|=4,|
|=1,S△ABC=
,则
•
的值为( )
| AB |
| AC |
| 3 |
| AB |
| AC |
| A、-2 | B、2 | C、±4 | D、±2 |