题目内容
 如图,在三棱锥B-ACD中,AB=BD=CD=1,AC=
如图,在三棱锥B-ACD中,AB=BD=CD=1,AC=| 3 |
(Ⅰ)求证:平面BDE⊥平面ACD;
(Ⅱ)求直线AC与平面ABD所成角的正弦值.
分析:(Ⅰ)要证平面BCE⊥平面ACD,需证BE⊥面ACD,即可.
(Ⅱ)求直线AC与平面ABD所成角的正弦值.用等体积方法求出C到面ABD的距离即可.
(Ⅱ)求直线AC与平面ABD所成角的正弦值.用等体积方法求出C到面ABD的距离即可.
解答:解:(Ⅰ)由已知得CE=
,DE=AE=
BE=
,
∴BE2+DE2=BD2,
∴BE⊥DE又∵BE⊥AC,∴BE⊥面ACD,
∵BE?,面BDE,
∴面BDE⊥面ACD
(Ⅱ)方法一:
设C到平面ABD的距离为h,由VB-ACD=VC-ABD,
得
S△ACD•BE=
S△ABD•h
则h=
=
=
.
设AC于平面ABD所成角为α,则sinα=
=
,
∴AC与平面ABD所成角的正弦值为
.
 方法二:建立如图所示直角坐标系,则
方法二:建立如图所示直角坐标系,则
D(0,0,0),A(
,-
,0),
B(
,0,
),C(0,1,0),
∴
=(-
,
,0),
=(
,-
,0)
=(
,0,
)
设平面ABD的一个法向量为n=(x,y,z),
则
∴取n=(
,
,-1)
设AB于平面ABD所成角为αsinα=
=
=
,
∴AC与平面ABD所成角的正弦值为
2
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
∴BE2+DE2=BD2,
∴BE⊥DE又∵BE⊥AC,∴BE⊥面ACD,
∵BE?,面BDE,
∴面BDE⊥面ACD
(Ⅱ)方法一:
设C到平面ABD的距离为h,由VB-ACD=VC-ABD,
得
| 1 |
| 3 |
| 1 |
| 3 |
则h=
| SACD•BE |
| S△ABD |
| ||||||||
|
| ||
| 3 |
设AC于平面ABD所成角为α,则sinα=
| h |
| AC |
| ||
| 3 |
∴AC与平面ABD所成角的正弦值为
| ||
| 3 |
 方法二:建立如图所示直角坐标系,则
方法二:建立如图所示直角坐标系,则D(0,0,0),A(
| ||
| 2 |
| 1 |
| 2 |
B(
| ||
| 3 |
| ||
| 3 |
∴
| AC |
| ||
| 2 |
| 3 |
| 2 |
| DA |
| ||
| 2 |
| 1 |
| 2 |
| DB |
| ||
| 3 |
| ||
| 3 |
设平面ABD的一个法向量为n=(x,y,z),
则
|
∴取n=(
| 2 |
| 6 |
设AB于平面ABD所成角为αsinα=
|
| ||
|
|
| ||
|
| ||
| 3 |
∴AC与平面ABD所成角的正弦值为
| ||
| 3 |
点评:本题考查空间直线和平面之间的位置关系,平面与平面之间的位置关系,空间直角坐标系的运算,是中档题.

练习册系列答案
相关题目
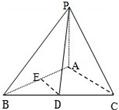 如图,在三棱锥P-ABC中,D、E分别是BC、AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是( )
如图,在三棱锥P-ABC中,D、E分别是BC、AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是( )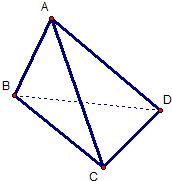 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD= 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4. 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC. 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,