题目内容
若△ABC中,三个内角A、B、C成等差数列,且a+c=1,则边b的取值范围是________.

分析:由题意可得B=
 ,A+C=
,A+C= ,由余弦定理可得 b2=1-3ac,利用基本不等式求出b≥
,由余弦定理可得 b2=1-3ac,利用基本不等式求出b≥ ,再由b<a+c=1,求出边b的取值范围.
,再由b<a+c=1,求出边b的取值范围.解答:若△ABC中,三个内角A、B、C成等差数列,则有B=
 ,A+C=
,A+C= .
.由余弦定理可得 b2=a2+c2-2ac•cosB=a2+c2-ac=(a+c)2-3ac=1-3ac.
∵a+c=1≥2
 ,∴ac≤
,∴ac≤ .
.∴b2=1-3ac≥
 ,即b≥
,即b≥ .
.再由b<a+c=1,可得
 ≤b<1,故边b的取值范围是
≤b<1,故边b的取值范围是 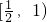 ,
,故答案为
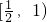 .
.点评:本题主要考查等差数列的定义和性质,余弦定理、基本不等式的应用,解三角形,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在棱锥P-ABC中,侧棱PA、PB、PC两两垂直,Q为底面△ABC内一点,若点Q到三个侧面的距离分别为3、4、5,则以线段PQ为直径的球的表面积为( )
| A、100π | ||
| B、50π | ||
| C、25π | ||
D、5
|