题目内容
如图所示,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP= ,求△POC面积的最大值及此时
,求△POC面积的最大值及此时 的值.
的值.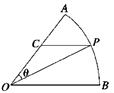
 ,求△POC面积的最大值及此时
,求△POC面积的最大值及此时 的值.
的值.
 =
=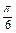 时,S(
时,S( )取得最大值为
)取得最大值为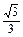
∵CP∥OB,∴∠CPO=∠POB=60°- ,
,
∠OCP=120°.
在△POC中,由正弦定理得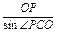 =
=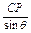 ,
,
∴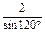 =
=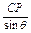 ,∴CP=
,∴CP=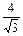 sin
sin .
.
又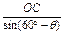 =
=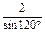 ,
,
∴OC=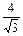 sin(60°-
sin(60°- ).
).
因此△POC的面积为
S( )=
)=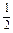 CP·OCsin120°
CP·OCsin120°
=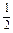 ·
·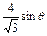 ·
·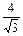 sin(60°-
sin(60°- )×
)×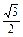
=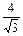 sin
sin sin(60°-
sin(60°- )
)
=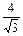 sin
sin (
(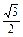 cos
cos -
-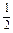 sin
sin )
)
=2sin ·cos
·cos -
-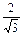 sin2
sin2
=sin2 +
+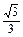 cos2
cos2 -
-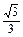
=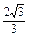 sin(2
sin(2 +
+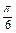 )-
)-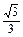 .
.
∴ =
=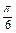 时,S(
时,S( )取得最大值为
)取得最大值为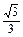 .
.
 ,
,∠OCP=120°.
在△POC中,由正弦定理得
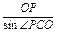 =
=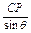 ,
,∴
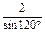 =
=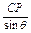 ,∴CP=
,∴CP=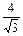 sin
sin .
.又
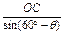 =
=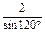 ,
,∴OC=
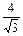 sin(60°-
sin(60°- ).
).因此△POC的面积为
S(
 )=
)=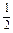 CP·OCsin120°
CP·OCsin120°=
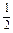 ·
·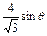 ·
·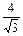 sin(60°-
sin(60°- )×
)×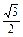
=
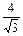 sin
sin sin(60°-
sin(60°- )
)=
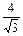 sin
sin (
(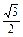 cos
cos -
-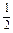 sin
sin )
)=2sin
 ·cos
·cos -
-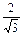 sin2
sin2
=sin2
 +
+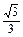 cos2
cos2 -
-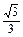
=
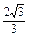 sin(2
sin(2 +
+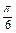 )-
)-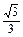 .
.∴
 =
=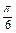 时,S(
时,S( )取得最大值为
)取得最大值为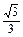 .
.
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
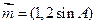 ,
,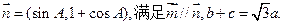 (I)求A的大小;(II)求
(I)求A的大小;(II)求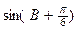 的值.
的值.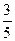 ,cosB=
,cosB=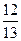 , 试判断三角形的形状.
, 试判断三角形的形状.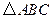 的面积为1,
的面积为1,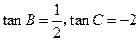 ,求
,求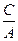 ,
,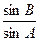 都是方程log
都是方程log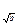 x=logb(4x-4)的根,则△ABC ( )
x=logb(4x-4)的根,则△ABC ( )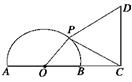 的延长线上,BC=1,点P为半圆上的一个动点,以
的延长线上,BC=1,点P为半圆上的一个动点,以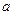 、
、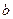 、
、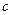 分别是角A、B、C所对的边,∠A=60º,
分别是角A、B、C所对的边,∠A=60º,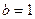 , △ABC的面积
, △ABC的面积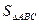 =
=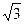 ,则
,则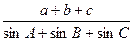 的值等于( )
的值等于( )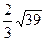 (B)
(B) 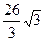 (C)
(C) 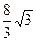 (D)
(D)