题目内容
函数y=lg（1-x）的定义域为A，函数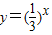
的值域为B，则A∩B=（ ）A．（0，1）
B．
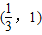
C．ϕ
D．R
【答案】分析：由题设知A={x|1-x＞0}={x|x＜1}，B={y|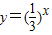
}={y|y＞0}，由此能求出A∩B．
解答：解：∵函数y=lg（1-x）的定义域为A，
函数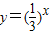
的值域为B，
∴A={x|1-x＞0}={x|x＜1}，
B={y|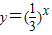
}={y|y＞0}，
∴A∩B={x|0＜x＜1}．
故选A．
点评：本题考查对数的定义域，是基础题，解题时要认真审题，仔细解答．
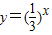}={y|y＞0}，由此能求出A∩B．解答：解：∵函数y=lg（1-x）的定义域为A，
函数
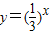的值域为B，∴A={x|1-x＞0}={x|x＜1}，
B={y|
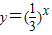}={y|y＞0}，∴A∩B={x|0＜x＜1}．
故选A．
点评：本题考查对数的定义域，是基础题，解题时要认真审题，仔细解答．
练习册系列答案
相关题目