题目内容
长方体ABCD-A1B1C1D1的八个顶点都在球O的球面上,其中AA1=1,AB=2
,AD=3
,则经过B、C两点的球面距离是
| 2 |
| 3 |
2π
2π
.分析:由长方体的对角线公式,算出对角线长为6,得到外接球半径R=3.在△OBC中,利用余弦定理算出∠BOC的大小,再结合球面距离公式即可得到经过B、C两点的球面距离.
解答:解:∵AA1=1,AB=2
,AD=3
,
∴长方体对角线AC1=
=6
∴长方体ABCD-A1B1C1D1的外接球直径为6,半径R=3,
设外接球心为O,△OBC中,BC=AD=3
,
∴cos∠BOC=
=-
,得∠BOC=
因此,经过B、C两点的球面距离为
R=2π
故答案为:2π
| 2 |
| 3 |
∴长方体对角线AC1=
| AA12+AB2+AD2 |
∴长方体ABCD-A1B1C1D1的外接球直径为6,半径R=3,
设外接球心为O,△OBC中,BC=AD=3
| 3 |
∴cos∠BOC=
32+32-(3
| ||
| 2×3×3 |
| 1 |
| 2 |
| 2π |
| 3 |
因此,经过B、C两点的球面距离为
| 2π |
| 3 |
故答案为:2π
点评:本题在长方体外接球中,求两点之间的球面距离,着重考查了长方体的性质和球面距离计算等知识,属于基础题.

练习册系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
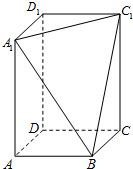 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.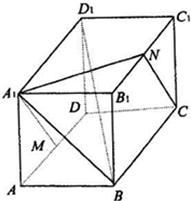 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.