题目内容
从5名男生和2名女生中选出3名志愿者,其中至少有1名女生被选中的方法数是
- A.10
- B.20
- C.25
- D.30
C
分析:至少有1名女生被选中包括有一名女生被选中和有两名女生被选中,当有一名女生被选中时有C21C52,当有两名女生被选中时有C22C51,由分类计数原理得到结果.
解答:∵至少有1名女生被选中包括有一名女生被选中和有两名女生被选中,
当有一名女生被选中时有C21C52=20,
当有两名女生被选中时有C22C51=5
由分类计数原理知共有20+5=25种结果,
故选C.
点评:对于复杂一点的计数问题,有时分类以后,每类方法并不都是一步完成的,必须在分类后又分步,综合利用两个原理解决,即类中有步,步中有类.
分析:至少有1名女生被选中包括有一名女生被选中和有两名女生被选中,当有一名女生被选中时有C21C52,当有两名女生被选中时有C22C51,由分类计数原理得到结果.
解答:∵至少有1名女生被选中包括有一名女生被选中和有两名女生被选中,
当有一名女生被选中时有C21C52=20,
当有两名女生被选中时有C22C51=5
由分类计数原理知共有20+5=25种结果,
故选C.
点评:对于复杂一点的计数问题,有时分类以后,每类方法并不都是一步完成的,必须在分类后又分步,综合利用两个原理解决,即类中有步,步中有类.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
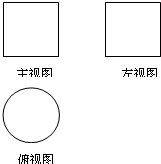 (文)如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为
(文)如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为