题目内容
 如图,椭
如图,椭 (a>b>0)的离心率e=
(a>b>0)的离心率e= ,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于
,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于
- A.3

- B.
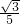
- C.-
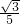
- D.-3

D
分析:根据离心率的值求出 和
和  的值,求得tan∠BAO=
的值,求得tan∠BAO= =
= 的值,再求出tan∠OFC=
的值,再求出tan∠OFC= =
= 的值,
的值,
代入tan∠BDC=tan(∠BAO+∠OFC) 进行运算.
解答:∵离心率e= ,∴
,∴ =
= =
= =
= ,
, =
= =
= .
.
由图可知,tan∠BDC=tan(∠BAO+∠OFC),∴tan∠BAO= =
= =
= ,
,
tan∠OFC= =
= =
= ,代入公式即得
,代入公式即得
tan∠BDC=tan(∠BAO+∠OFC)= =-3
=-3 ,
,
故选 D.
点评:本题考查椭圆的简单性质的应用,两角和差的正切函数,判断tan∠BDC=tan(∠BAO+∠OFC),是解题的难点和
关键.
分析:根据离心率的值求出
 和
和  的值,求得tan∠BAO=
的值,求得tan∠BAO= =
= 的值,再求出tan∠OFC=
的值,再求出tan∠OFC= =
= 的值,
的值,代入tan∠BDC=tan(∠BAO+∠OFC) 进行运算.
解答:∵离心率e=
 ,∴
,∴ =
= =
= =
= ,
, =
= =
= .
.由图可知,tan∠BDC=tan(∠BAO+∠OFC),∴tan∠BAO=
 =
= =
= ,
,tan∠OFC=
 =
= =
= ,代入公式即得
,代入公式即得 tan∠BDC=tan(∠BAO+∠OFC)=
 =-3
=-3 ,
,故选 D.
点评:本题考查椭圆的简单性质的应用,两角和差的正切函数,判断tan∠BDC=tan(∠BAO+∠OFC),是解题的难点和
关键.

练习册系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: 如图,F1,F2为椭圆C:
如图,F1,F2为椭圆C:
 的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
 ;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点
;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是( )
时AM过椭圆的右焦点.其中所有的真命题是( )