题目内容
椭圆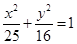 的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2下面结论正确的是( )
的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2下面结论正确的是( )
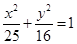 的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2下面结论正确的是( )
的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2下面结论正确的是( )| A.P点有两个 | B.P点有四个 |
| C.P点不一定存在 | D.P点一定不存在 |
D
不妨设椭圆 的焦点
的焦点 ,设
,设 ,因为
,因为 ,所以
,所以 ,即
,即 ,则
,则 ,所以点
,所以点 在以原点为圆心3为半径的圆上。而椭圆
在以原点为圆心3为半径的圆上。而椭圆 与圆
与圆 没有交点,所以符合条件的点
没有交点,所以符合条件的点 不存在,故选D
不存在,故选D
 的焦点
的焦点 ,设
,设 ,因为
,因为 ,所以
,所以 ,即
,即 ,则
,则 ,所以点
,所以点 在以原点为圆心3为半径的圆上。而椭圆
在以原点为圆心3为半径的圆上。而椭圆 与圆
与圆 没有交点,所以符合条件的点
没有交点,所以符合条件的点 不存在,故选D
不存在,故选D
练习册系列答案
相关题目
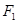 、
、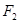 分别是椭圆
分别是椭圆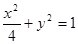 的左、右焦点.
的左、右焦点. 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求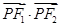 的最大值和最小值;
的最大值和最小值; 的直线
的直线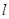 与椭圆交于不同的两点
与椭圆交于不同的两点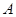 、
、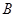 ,且∠
,且∠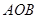 为锐角(其中
为锐角(其中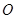 为坐标原点),求直线
为坐标原点),求直线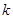 的取值范围.
的取值范围.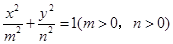 的右焦点为
的右焦点为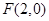 ,离心率为
,离心率为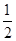 ,则此椭圆的方程为___________
,则此椭圆的方程为___________ 是椭圆
是椭圆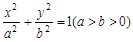 上的一动点,且
上的一动点,且 ,则椭圆离心率为 ( )
,则椭圆离心率为 ( )



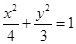 上任意一点,F1、F2是焦点,那么∠F1PF2的最大值是( )
上任意一点,F1、F2是焦点,那么∠F1PF2的最大值是( )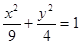 上的点,F1、F2是两个焦点,则|PF1|·|PF2|的最大值与最小值之差是______.
上的点,F1、F2是两个焦点,则|PF1|·|PF2|的最大值与最小值之差是______. ,
, 是椭圆上关于原点对称的两点,
是椭圆上关于原点对称的两点, 是椭圆上任意一点且直线
是椭圆上任意一点且直线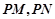 的斜率分别为
的斜率分别为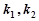 ,
,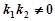 ,则
,则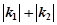 的最小值为
的最小值为 ,则椭圆的离心率为( ).
,则椭圆的离心率为( ).



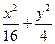 =1内一点(2,1)的弦被该点平分,则该弦所在直线的方程是______
=1内一点(2,1)的弦被该点平分,则该弦所在直线的方程是______