题目内容
已知等差数列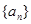 满足:
满足: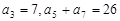 ,
,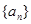 的前n项和为
的前n项和为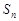 .
.
(1)求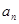 及
及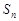 ;
;
(2)令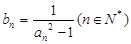 ,求数列
,求数列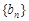 的前n项和
的前n项和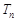 .
.
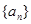 满足:
满足: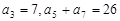 ,
,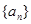 的前n项和为
的前n项和为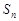 .
.(1)求
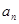 及
及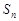 ;
;(2)令
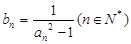 ,求数列
,求数列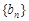 的前n项和
的前n项和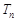 .
.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)等差数列问题常可转化为其基本量首项和公差的问题,这是最基本的思路,但有时如果充分利用等差数列的性质,可能达到简化计算的目的,本题可用首项和公差表示
 ,解之即得首项和公差,然后再用等差数列的通项公式和前
,解之即得首项和公差,然后再用等差数列的通项公式和前 项的和公式求出结果;(2)把(1)中的结果
项的和公式求出结果;(2)把(1)中的结果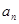 代入
代入 ,再根据其特征选择合适的方法求前n项和
,再根据其特征选择合适的方法求前n项和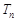 ,本题是利用裂项相消法求和.
,本题是利用裂项相消法求和.试题解析:(1)设等差数列
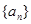 的首项为
的首项为 ,公差为
,公差为 , 1分
, 1分由
 ,解得
,解得 . 5分
. 5分由于
 ,所以
,所以 . 7分
. 7分(2)因为
 ,所以
,所以 ,因此
,因此 . 9分
. 9分故
 , 13分
, 13分所以数列
 的前n项和
的前n项和
 . 14分
. 14分
练习册系列答案
相关题目
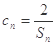 ,数列{cn}的前n项和为Tn,求证
,数列{cn}的前n项和为Tn,求证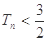
 满足:
满足: ,
, .
. 及
及 的第n项为
的第n项为 ,若
,若 成等差数列,且
成等差数列,且 ,设数列
,设数列 的前
的前 项和
项和 .求数列
.求数列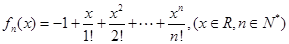
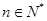 ,存在唯一的
,存在唯一的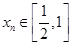 ,满足
,满足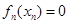 ;
;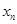 构成数列
构成数列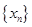 ,判断数列
,判断数列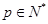 ,
,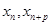 满足(Ⅰ),试比较
满足(Ⅰ),试比较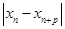 与
与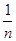 的大小.
的大小.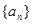 是等差数列,且
是等差数列,且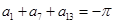 ,则
,则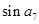 =
=  的公差
的公差 ,前
,前 项和
项和 满足:
满足: ,那么数列
,那么数列 中最大的值是( )
中最大的值是( )



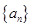 为等比数列,且
为等比数列,且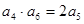 ,设等差数列
,设等差数列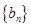 的前n项和为
的前n项和为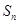 ,若
,若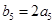 ,则
,则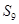 =( )
=( ) 的首项
的首项 ,若
,若 ,
, ,则
,则 .
.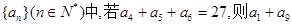 等于( )
等于( )