题目内容
已知等差数列 满足:
满足: ,
, 的前n项和为
的前n项和为 .
.
(1)求 及
及 ;
;
(2)已知数列 的第n项为
的第n项为 ,若
,若 成等差数列,且
成等差数列,且 ,设数列
,设数列 的前
的前 项和
项和 .求数列
.求数列 的前
的前 项和
项和 .
.
 满足:
满足: ,
, 的前n项和为
的前n项和为 .
.(1)求
 及
及 ;
;(2)已知数列
 的第n项为
的第n项为 ,若
,若 成等差数列,且
成等差数列,且 ,设数列
,设数列 的前
的前 项和
项和 .求数列
.求数列 的前
的前 项和
项和 .
.(1) ,
, ; (2)
; (2) .
.
 ,
, ; (2)
; (2) .
.试题分析:(1)由
 根据等差中项的性质求得
根据等差中项的性质求得 ,结合
,结合 可以求得
可以求得 和
和 ,再将
,再将 和
和 代入等差数列的通项公式化简整理即可,然后由等差数列的前
代入等差数列的通项公式化简整理即可,然后由等差数列的前 项和公式求得
项和公式求得 ;(2)根据等差数列的等差中项的性质,结合
;(2)根据等差数列的等差中项的性质,结合 可以得到
可以得到 ,由迭代法求数列
,由迭代法求数列 的通项公式
的通项公式 ,注意讨论
,注意讨论 是否符合此通项公式,观察式子特点
是否符合此通项公式,观察式子特点 ,利用裂项相消的原则求数列
,利用裂项相消的原则求数列 的前
的前 项和
项和 .
.试题解析:(1)设等差数列
 的公差为
的公差为 ,
,因为
 ,
, ,所以
,所以 . 2分
. 2分则
 ,
, ,
,所以
 ; 4分
; 4分 . 6分
. 6分(2)由(1)知
 ,
,因为
 成等差数列,
成等差数列,所以

 ,即
,即 ,
,所以
 . 8分
. 8分故



 .
.又因为
 满足上式,所以
满足上式,所以 10分
10分所以
 .
.故

 .12分
.12分 项和;3.数列的递推公式;4.数列的求和
项和;3.数列的递推公式;4.数列的求和
练习册系列答案
相关题目
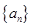 满足
满足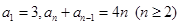
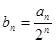 ,求数列
,求数列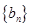 的前
的前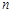 项和
项和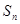 .
.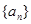 满足:
满足: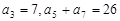 ,
,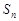 .
.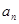 及
及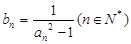 ,求数列
,求数列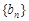 的前n项和
的前n项和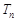 .
. 为等差数列,且
为等差数列,且 ,
, 为
为 项和.
项和. 及
及 ,求数列
,求数列 的通项公式
的通项公式 及其前
及其前 .
.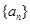 的前
的前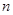 项和是
项和是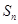 且
且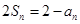
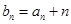 ,求数列
,求数列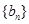 的前
的前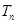 .
. 为等差数列
为等差数列 的前
的前 项和,
项和, ,则
,则 = ( )
= ( )


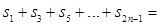 .
.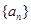 的前n项和为
的前n项和为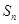 ,若
,若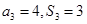 ,则公差
,则公差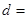 ___________.
___________. 排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )
排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )