题目内容
18. 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,点M,N分别是AB,PC的中点,且PA=AD
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,点M,N分别是AB,PC的中点,且PA=AD(1)求证:MN∥平面PAD
(2)求证:平面PMC⊥平面PCD.
分析 (1)设PD的中点为点E,连接AE,NE,可得AMNE是平行四边形,即可得MN∥平面PAD
(2)由AE⊥PD,CD⊥AE,得AE⊥平面PCD,结合MN∥AE,可得MN⊥平面PCD,即可证得平面PMC⊥平面PCD
解答 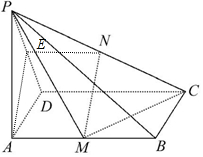 解:(1)设PD的中点为点E,连接AE,NE,
解:(1)设PD的中点为点E,连接AE,NE,
由点N为PC的中点知EN∥$\frac{1}{2}$DC,EN=$\frac{1}{2}$DC,
又ABCD是矩形,所以DC∥AB,DC=AB,所以EN∥$\frac{1}{2}$AB,EN=$\frac{1}{2}$AB,
又点M是AB的中点,所以EN∥AM,EN=AM,所以AMNE是平行四边形,
所以MN∥AE,而AE?平面PAD,NM?平面PAD,所以MN∥平面PAD.(6分)
(2)因为PA=AD,所以AE⊥PD,又因为PA⊥平面ABCD,CD?平面ABCD,
所以CD⊥PA,而CD⊥AD,所以CD⊥平面PAD,所以CD⊥AE,因为PD∩CD=D,
所以AE⊥平面PCD,因为MN∥AE,所以MN⊥平面PCD,
又MN?平面PMC,所以平面PMC⊥平面PCD.(12分)
点评 本题考查了空间线面平行的判定,面面垂直的判定,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在等比数列{an}中,S3=1,S6=4,则a10+a11+a12的值是( )
| A. | 81 | B. | 64 | C. | 32 | D. | 27 |
13.已知数列{an}满足an+1=an-an-1(n≥2),a1=2017,a2=2016,Sn为数列{an}的前n项和,则S2017的值为( )
| A. | 2017×2016 | B. | 2016 | C. | 2017 | D. | 1 |
3.若将函数y=sin(2x+φ)图象向右平移$\frac{π}{8}$个单位长度后关于y轴对称,则φ的值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{8}$ |
7.为了调查高中学生是否喜欢数学与性别的关系,随机抽查男、女学生各 40 名,得到具体数据如表:
(I)根据上面的列联表,能否在犯错误的概率不超过 0.025 的前提下,认为是否喜欢数学与性别有关?
(II)计算这 80 位学生不喜欢数学的频率;(III)用分层抽样的方法从不喜欢数学的男女学生中抽查 6 人进行数学问卷调查,再从中抽取 4 份问卷递交校长办,求至少抽出 3 名女生问卷的概率.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| 是否喜欢数学 | 是 | 否 | 合计 |
| 男生 | 30 | 10 | 40 |
| 女生 | 20 | 20 | 40 |
| 合计 | 50 | 30 | 80 |
(II)计算这 80 位学生不喜欢数学的频率;(III)用分层抽样的方法从不喜欢数学的男女学生中抽查 6 人进行数学问卷调查,再从中抽取 4 份问卷递交校长办,求至少抽出 3 名女生问卷的概率.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0[来源:] | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
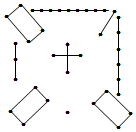 洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.
洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.