题目内容
已知集合 是同时满足下列两个性质的函数
是同时满足下列两个性质的函数 组成的集合:①
组成的集合:① 在其定义域上是单调增函数或单调减函数;②在
在其定义域上是单调增函数或单调减函数;②在 的定义域内存在区间,使得
的定义域内存在区间,使得 在
在 上的值域是
上的值域是 .
.
(1)判断函数 是否属于集合
是否属于集合 ?若是,则求出
?若是,则求出 .若不是,说明理由;
.若不是,说明理由;
(2)若函数 求实数
求实数 的取值范围.
的取值范围.
(1)
(2)
【解析】
试题分析:(1)若函数 属于集合
属于集合 ,由①、②可得
,由①、②可得 ,解出
,解出 即可;(2)利用函数
即可;(2)利用函数 ,令
,令 ,化为关于
,化为关于 的二次函数根的分布问题求解即可.
的二次函数根的分布问题求解即可.
试题解析:(1)①因为 在
在 上为增函数;
上为增函数;
②假设存在区间 ,则有
,则有 ,
,
∴  是方程
是方程 的两个不同的非负根,∴
的两个不同的非负根,∴ ,
,
∴  属于集合
属于集合 ,且
,且 .
.
(2)①∵ 在
在 上为增函数,
上为增函数,
②设区间 ,则有
,则有 ,
,
∴ 是方程
是方程 的两个不同的根,且
的两个不同的根,且 ,
,
令
∴ 即
即 有两个不同的非负实根,
有两个不同的非负实根,
∴ ,解得
,解得 .
.
考点:(1)元素与集合的关系,方程的思想;(2)函数单调性,方程思想以及二次方程根的分布.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
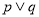 为真”是命题“
为真”是命题“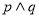 为真”的
为真”的 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴都相切,则该圆的标准方程是 .
轴都相切,则该圆的标准方程是 . 的性质,构造了如图所示的两个边长为
的性质,构造了如图所示的两个边长为 的正方形
的正方形 和
和 ,点
,点 是边
是边 上的一个动点,设
上的一个动点,设 ,则
,则 .此时
.此时 = .
= .
 中,
中, 与平面
与平面 所成的角为
所成的角为 ,则
,则 所成的角为 .(结果用反三角函数表示)
所成的角为 .(结果用反三角函数表示)
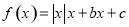 ,给出下列4个命题:①
,给出下列4个命题:①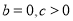 时,方程
时,方程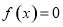 只有一个实数根;②
只有一个实数根;②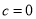 时,
时,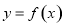 是奇函数;③
是奇函数;③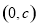 对称;④方程
对称;④方程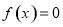 至多有2个不相等的实数根.上述命题中的所有正确命题的序号是 .
至多有2个不相等的实数根.上述命题中的所有正确命题的序号是 . 满足:当
满足:当 时,有
时,有 .给出以下三个命题:①若
.给出以下三个命题:①若 ,则
,则 ;②若
;②若 ,则
,则 ;③若
;③若 ,则
,则 .其中正确的命题个数是( )
.其中正确的命题个数是( ) 中,若
中,若 ,则数列的通项
,则数列的通项 .
. 的焦点
的焦点 和点
和点 ,
, 为抛物线上一点,则
为抛物线上一点,则 的最小值是______________
的最小值是______________