题目内容
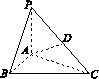
[2012·上海卷] 如图1－1，在三棱锥P－ABC中，PA⊥底面ABC，D是PC的中点，已知∠BAC＝
，AB＝2，AC＝2
，PA＝2，求：
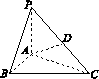
图1－1
(1)三棱锥P－ABC的体积；
(2)异面直线BC与AD所成的角的大小(结果用反三角函数值表示)．
解：(1)S△ABC＝
×2×2＝2，
图1－2
三棱锥P－ABC的体积为
V＝
S△ABC×PA＝×2×2＝
.
(2)取PB的中点E，连接DE、AE，则ED∥BC，所以∠ADE(或其补角)是异面直线BC与AD所成的角．
在△ADE中，DE＝2，AE＝
，AD＝2，
cos∠ADE＝
＝
，
所以∠ADE＝arccos.
因此，异面直线BC与AD所成的角的大小是arccos.
练习册系列答案
相关题目
，AB＝2，AC＝2
，PA＝2，求：
轴正方向建立平面直角坐标系（以1海里为单位长度），则救援船恰好在失事船正南方向12海里
处，如图．现假设：①失事船的移动路径可视为抛物线
；②定位后救援船即刻沿直线匀速前往救援；③救援船出发
小时后，失事船所在位置的横坐标为
．
时，写出失事船所在位置
的纵坐标．若此时两船恰好会合，求
中，已知双曲线
：
．
轴围成的三角形的面积；
交
两点，若
相切，求证：
；
：
，若
、
分别是
，求证：
到直线
的距离是定值.