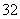题目内容
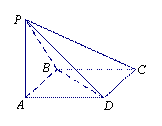
如图,在四棱锥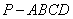 中,底面
中,底面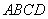 是边长为
是边长为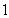 的正方形,
的正方形,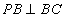 ,
,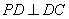 ,且
,且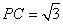 .
.
(Ⅰ)求证: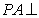 平面
平面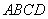 ;
;
(Ⅱ)求二面角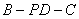 的余弦值;
的余弦值;
(Ⅲ)棱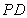 上是否存在一点
上是否存在一点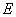 ,使直线
,使直线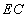 与平面
与平面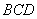 所成的角是
所成的角是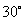 ?若存在,求
?若存在,求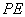 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(Ⅰ)证明:在正方形 中,
中,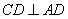 .
.
因为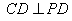 ,
,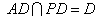 ,
,
所以 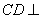 平面
平面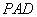 .
.
因为 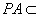 平面
平面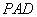 ,
,
所以 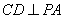 .
.
同理,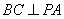 .
.
因为 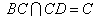 ,
,
所以 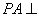 平面
平面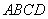 .
.
(Ⅱ)解:连接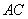 ,由(Ⅰ)知
,由(Ⅰ)知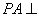 平面
平面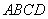 .
.
因为 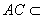 平面
平面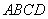 ,
,
所以 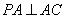 .
.
因为 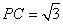 ,
,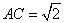 ,
,
所以 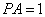 .
.
分别以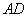 ,
,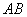 ,
,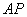 所在的直线分别为
所在的直线分别为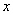 ,
,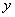 ,
,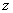 轴,建立空间直角坐标系,如图所示.
轴,建立空间直角坐标系,如图所示.
由题意可得: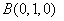 ,
,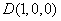 ,
,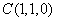 ,
,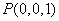 .
.
所以 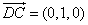 ,
,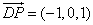 ,
,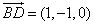 ,
,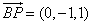 .
.
设平面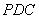 的一个法向量
的一个法向量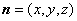 ,
,
则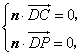 即
即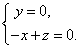 令
令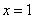 ,得
,得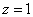 .
.
所以 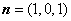 .
.
同理可求:平面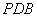 的一个法向量
的一个法向量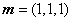 .
.
所以 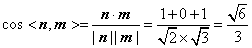 .
.
所以 二面角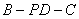 的余弦值为
的余弦值为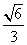 .
.
(Ⅲ)存在.理由如下:
若棱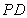 上存在点
上存在点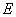 满足条件,设
满足条件,设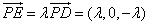 ,
,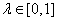 .
.
所以 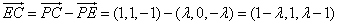 .
.  因为 平面
因为 平面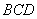 的一个法向量为
的一个法向量为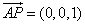 .
.
所以 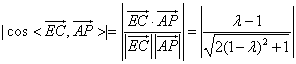 .
.
令 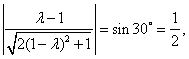 解得:
解得: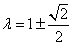 .
.
经检验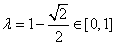 .
.
所以 棱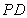 上存在点
上存在点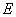 ,使直线
,使直线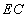 与平面
与平面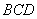 所成的角是
所成的角是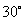 ,此时
,此时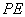 的长为
的长为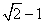 .
.

已知函数满足,当时,,若在区间上方程有两个不同的实根,则实数的取值范围是( )
| A. | B. | C. | D. |
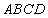 中,
中,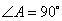 ,
,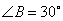 ,
,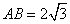 ,
,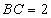 ,点
,点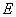 在线段
在线段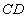 上,若
上,若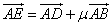 ,则
,则 的取值范围是
的取值范围是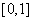 (B)
(B)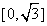 (C)
(C)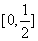 (D)
(D)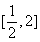
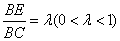 ,则满足
,则满足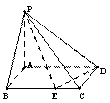
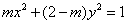 表示焦点在
表示焦点在 的取值范围是( )
的取值范围是( )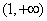 (B)
(B)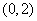 (C)
(C)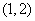 (D)
(D)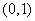
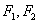 是双曲线
是双曲线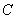 的两个焦点,过点
的两个焦点,过点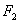 的直线交双曲线
的直线交双曲线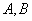 两点,若
两点,若 为等边三角形,则双曲线
为等边三角形,则双曲线 的值为6,那么运行相应程序,输出的
的值为6,那么运行相应程序,输出的 的值为
的值为 A. 3 B. 5 C. 10 D. 16
A. 3 B. 5 C. 10 D. 16 :
: (
( 为参数)的圆心坐标为__________;直线
为参数)的圆心坐标为__________;直线 :
: 被圆
被圆 B.
B.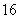 C.
C.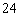 D.
D.