题目内容
(本小题满分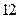 分)在平面直角坐标系中,已知两个定点
分)在平面直角坐标系中,已知两个定点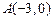 和
和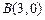 .动点
.动点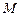 在
在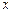 轴上的射影是
轴上的射影是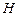 (
(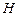 随
随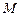 移动而移动),若对于每个动点M总存在相应的点
移动而移动),若对于每个动点M总存在相应的点 满足
满足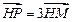 ,且
,且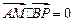 .
.
(Ⅰ)求动点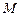 的轨迹
的轨迹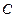 的方程;
的方程;
(Ⅱ)设过定点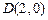 的直线
的直线 (直线
(直线 与
与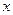 轴不重合)交曲线
轴不重合)交曲线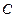 于
于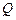 ,
,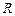 两点,求证:直线
两点,求证:直线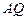 与直线
与直线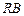 交点总在某直线
交点总在某直线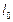 上.
上.
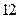 分)在平面直角坐标系中,已知两个定点
分)在平面直角坐标系中,已知两个定点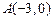 和
和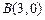 .动点
.动点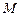 在
在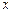 轴上的射影是
轴上的射影是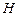 (
(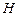 随
随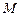 移动而移动),若对于每个动点M总存在相应的点
移动而移动),若对于每个动点M总存在相应的点 满足
满足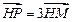 ,且
,且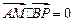 .
.(Ⅰ)求动点
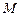 的轨迹
的轨迹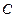 的方程;
的方程;(Ⅱ)设过定点
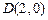 的直线
的直线 (直线
(直线 与
与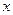 轴不重合)交曲线
轴不重合)交曲线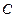 于
于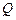 ,
,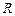 两点,求证:直线
两点,求证:直线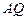 与直线
与直线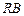 交点总在某直线
交点总在某直线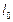 上.
上.(1) ;(2)略
;(2)略
 ;(2)略
;(2)略(Ⅰ)设 ,则
,则 ,
, ,
, ,
, ,
,
由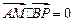 ,得
,得 ,
,
即轨迹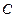 的方程为
的方程为 .--------4分
.--------4分
(Ⅱ)若直线 的斜率为
的斜率为 时,直线
时,直线 :
: ,设
,设 ,
, .
.
联立 ,得
,得 ,
,
即 ,
, ---------------5分
---------------5分
观察得, ,
,
即 ,
,
直线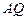 :
: ,直线
,直线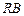 :
: ,
,
联立: ,
,
解之:

 ;所以
;所以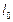 :
: ;
;
若
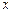 轴时,不妨得
轴时,不妨得 ,
, ,则此时,
,则此时,
直线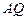 :
: ,直线
,直线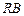 :
: ,
,
联立 ,解之
,解之 ,
, ,即交点也在直线
,即交点也在直线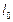 :
: 上.------12分
上.------12分
 ,则
,则 ,
, ,
, ,
, ,
,由
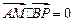 ,得
,得 ,
,即轨迹
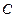 的方程为
的方程为 .--------4分
.--------4分(Ⅱ)若直线
 的斜率为
的斜率为 时,直线
时,直线 :
: ,设
,设 ,
, .
.联立
 ,得
,得 ,
,即
 ,
, ---------------5分
---------------5分观察得,
 ,
,即
 ,
,直线
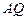 :
: ,直线
,直线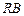 :
: ,
,联立:
 ,
,解之:


 ;所以
;所以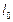 :
: ;
;若

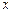 轴时,不妨得
轴时,不妨得 ,
, ,则此时,
,则此时,直线
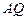 :
: ,直线
,直线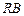 :
: ,
,联立
 ,解之
,解之 ,
, ,即交点也在直线
,即交点也在直线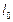 :
: 上.------12分
上.------12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,设
中,设 .
.  且
且 ,求
,求 的取值范围.
的取值范围.  ,
, ,且
,且 ⊥
⊥ ,则
,则 等于( )
等于( )



 ,若
,若 ,则
,则 的夹角为( )
的夹角为( )



 ,向量
,向量 ,且
,且 ,则
,则 的值是 .
的值是 . ,且
,且 与
与 的夹角为锐角,则实数
的夹角为锐角,则实数 的取值范围是 .
的取值范围是 . ,a·( a+b)=
,a·( a+b)= D.4+2
D.4+2 ,
, ,
, 满足
满足 ,
, ,
, ,
,
 ,则
,则 =
= ,
, =
= ,则
,则 在
在