题目内容
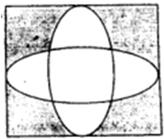 如图,已知正方形的边长为10,向正方形内随机地撒200颗黄豆,数得落在阴影外的黄豆数为114颗,以此实验数据为依据,可以估计出阴影部分的面积约为( )
如图,已知正方形的边长为10,向正方形内随机地撒200颗黄豆,数得落在阴影外的黄豆数为114颗,以此实验数据为依据,可以估计出阴影部分的面积约为( )| A、53 | B、43 | C、47 | D、57 |
分析:本题利用几何概型求解.由于是向正方形内随机地撒200颗黄豆,其落在阴影外的概率是阴影外的面积与整个正方形的面积之比,从而可列式求得阴影部分的面积.
解答:解:设阴影外部分的面积为s,
则由几何概型的概率公式得:
=
,
解得s=57,
可以估计出阴影部分的面积约为100-57=43.
故选B.
则由几何概型的概率公式得:
| s |
| 10×10 |
| 114 |
| 200 |
解得s=57,
可以估计出阴影部分的面积约为100-57=43.
故选B.
点评:本题主要考查了几何概型,以及利用几何意义求面积,属于基础题.简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.

练习册系列答案
相关题目
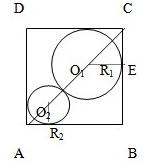 如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.
如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.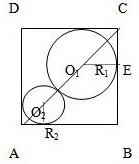 第8题的题干为:如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.
第8题的题干为:如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆. 的边长为
的边长为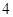 ,
,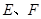 分别是
分别是 的中点,
的中点,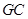 ⊥平面
⊥平面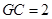 ,则点
,则点 到平面
到平面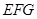 的距离为
的距离为 
 B.
B. C.
C.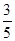 D.1
D.1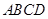 的边长为1,
的边长为1,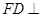 平面
平面 平面
平面 为
为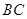 边上的动点。
边上的动点。 平面
平面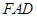 ;
; 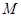 的位置,使平面
的位置,使平面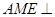 平面
平面 。
。