题目内容
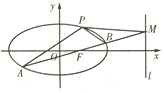
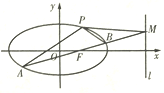
【题目】如图，椭圆
经过点
，离心率
，直线
的方程为
.
求椭圆
的方程；
是经过右焦点
的任一弦（不经过点
），设直线
与直线
相交于点
，记
， 
， 
的斜率为
， 
， 
.问：是否存在常数
，使得
？若存在，求
的值；若不存在，说明理由.
【答案】(Ⅰ) 
；(Ⅱ)存在常数
符合题意.
【解析】试题分析：（1）根据离心率得a,b,c三者关系，再将P点坐标代入椭圆方程，解得
， 
.（2）先根据两点斜率公式化简
，以及
，再利用直线方程与椭圆方程联立方程组，结合韦达定理化简
，最后作商得
的值
试题解析： 
由
在椭圆上得， 
①
依题设知
，则
②
②带入①解得
， 
， 
.
故椭圆
的方程为
.
由题意可设
的斜率为
，
则直线
的方程为
③
代入椭圆方程
并整理，得
，
设
， 
，则有
， 
④
在方程③中令
得， 
的坐标为
.
从而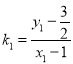
， 
， 
.
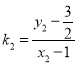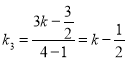注意到
， 
， 
共线，则有
，即有
.
所以
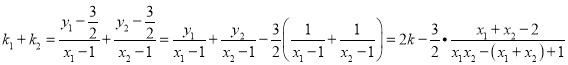⑤
④代入⑤得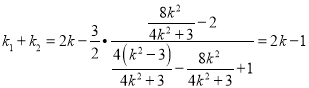
，
又
，所以
，故存在常数
符合题意.
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
