题目内容
不等式（a-2）x2+2（a-2）x-4＜0对一切x∈R恒成立，则实数a的取值范围是 ．
【答案】分析：当a-2=0，a=2时不等式即为-4＜0，对一切x∈R恒成立，当a≠2时 利用二次函数的性质列出a满足的条件并计算，最后两部分的合并即为所求范围．
解答：解：当a-2=0，a=2时不等式即为-4＜0，对一切x∈R恒成立 ①
当a≠2时，则须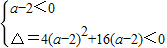
即
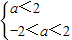∴-2＜a＜2 ②
由①②得实数a的取值范围是（-2，2]
故答案为：（-2，2]
点评：本题考查不等式恒成立的参数取值范围，考查二次函数的性质．注意对二次项系数是否为0进行讨论．
解答：解：当a-2=0，a=2时不等式即为-4＜0，对一切x∈R恒成立 ①
当a≠2时，则须
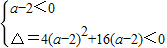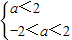即∴-2＜a＜2 ②由①②得实数a的取值范围是（-2，2]
故答案为：（-2，2]
点评：本题考查不等式恒成立的参数取值范围，考查二次函数的性质．注意对二次项系数是否为0进行讨论．
练习册系列答案
浙江名校名师金卷系列答案
相关题目