题目内容
【题目】某商场购进一种每件价格为90元的新商品，在商场试销时发现：销售单价
（元/件）与每天销售量
（件）之间满足如图所示的关系．
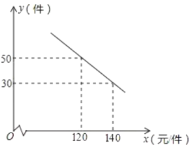
（1）求出与之间的函数关系式；
（2）写出每天的利润
与销售单价之间的函数关系式，并求出售价定为多少时，每天获得的利润最大？最大利润是多少？
【答案】（1）
；（2）售价定为130元时，每天获得的利润最大，最大利润是1600元．
【解析】
（1）先利用待定系数法求一次函数解析式；
（2）用每件的利润乘以销售量得到每天的利润
，即
，然后根据二次函数的性质解决问题．
（1）设
与
之间的函数关系式为
，
根据题意得
，解得
，
与之间的函数关系式为；
（2）
，
，
当
时，有最大值1600．
答：售价定为130元时，每天获得的利润最大，最大利润是1600元．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
零件的个数 |
|
|
|
|
加工的时间 |
|
|
|
|
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出
关于
的线性回归方程
.
（3）试预测加工
个零件需要多少时间？
附录：参考公式：
，
.
