题目内容
已知数列 的通项公式为
的通项公式为 ,其前
,其前 项和
项和 ,则双曲线
,则双曲线 的渐近线方程为( )
的渐近线方程为( )
A. | B. | C. | D. |
C
解析试题分析:根据数列 的通项公式为
的通项公式为 ,其前
,其前 项和
项和 ,那么可知
,那么可知 ,可知n=9,那么根据
,可知n=9,那么根据 可知a=
可知a= ,b= 3,故可知双曲线
,b= 3,故可知双曲线 的渐近线方程为
的渐近线方程为 ,选C.
,选C.
考点:数列的求和,双曲线的性质
点评:主要是考查了数列的通项公式和双曲线的性质的运用,属于基础题。

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
设函数 ,数列
,数列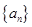 满足
满足 ,且数列
,且数列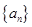 为递增数列,则实数A的取值范围为( )
为递增数列,则实数A的取值范围为( )
| A.(2,3) | B.(1,3) | C.(1,+ ) ) | D.(2, + ) ) |
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第 行有
行有 个数且两端的数均为
个数且两端的数均为
 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如 ,
, ,
, , ,则第10行第4个数(从左往右数)为( )
, ,则第10行第4个数(从左往右数)为( )
A. | B. |
C. | D. |
已知数列 满足
满足 ,
, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
若1既是 与
与 的等比中项,又是
的等比中项,又是 与
与 的等差中项,则
的等差中项,则 的值是 ( )
的值是 ( )
A.1或 | B.1或 | C.1或 | D.1或 |
数列 的通项公式为
的通项公式为 ,若其图像上存在点
,若其图像上存在点 在可行域
在可行域 内,则
内,则 的取值范围为
的取值范围为
A. | B. | C. | D. |
数列 的前项和为
的前项和为 ,则
,则 的值依次为( )
的值依次为( )
| A.3,4 | B.2,8 | C.3,18 | D.3,14 |
数列{an}中,an=-2n2+29n+3,则此数列最大项的值是( )
| A.103 | B.108 | C.103 | D.108 |
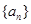 满足
满足 ,则
,则 .
.