题目内容
椭圆T: =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=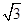 (x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
(x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
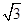 -1
-1
解析

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
题目内容
椭圆T: =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=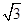 (x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
(x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
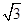 -1
-1
解析

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案