题目内容
(本小题满分12分)已知在四棱锥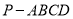 中,底面
中,底面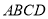 是矩形,且
是矩形,且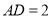 ,
,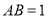 ,
,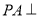 平面
平面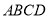 ,
, ,
,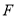 分别是线段
分别是线段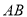 ,
,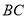 的中点.
的中点.

(1)判断并说明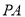 上是否存在点
上是否存在点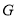 ,使得
,使得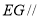 平面
平面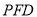 ?若存在,求出
?若存在,求出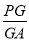 的值;若不
的值;若不
存在,请说明理由;
(2)若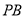 与平面
与平面 所成的角为
所成的角为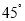 ,求二面角
,求二面角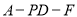 的平面角的余弦值.
的平面角的余弦值.
(1)存在,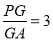 ;(2)
;(2)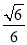 .
.
【解析】
试题分析:(1)根据四棱锥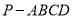 中,
中,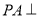 底面
底面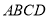 ,底面
,底面 是矩形可知,可以通过建立空间直角坐标系来求解问题,设
是矩形可知,可以通过建立空间直角坐标系来求解问题,设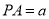 ,
, ,根据条件中给出的数据可得
,根据条件中给出的数据可得 ,从而可求得平面
,从而可求得平面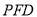 的一个法向量
的一个法向量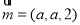 ,再由
,再由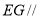 平面
平面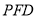 ,可知
,可知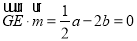 ,可得
,可得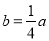 ,因此存在满足条件的点
,因此存在满足条件的点 ,且
,且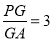 ;(2)由
;(2)由 与平面
与平面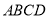 所成的角为
所成的角为 可知
可知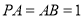 ,结合(1)可知平面
,结合(1)可知平面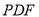 的一个法向量为
的一个法向量为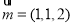 ,再取平面
,再取平面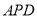 的一个法向量为
的一个法向量为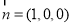 ,可求得
,可求得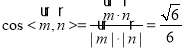 ,即二面角
,即二面角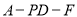 的平面角的余弦值为
的平面角的余弦值为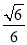 .
.
试题解析:(1)建立如图所示的空间直角坐标系,设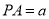 ,
, ,
,
∵ ,∴
,∴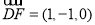 ,
,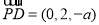 ,
,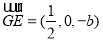 ,
,
设平面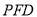 的一个法向量
的一个法向量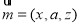 ,∴
,∴ ,∴
,∴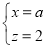 ,∴
,∴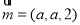 ,
,
∵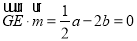 ,∴
,∴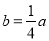 ,∴
,∴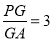 ;(2)∵
;(2)∵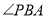 为直线
为直线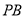 与平面
与平面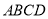 所成的角,
所成的角,
∴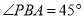 ,∵
,∵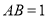 ,∴
,∴ ,由(1)知,平面
,由(1)知,平面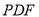 的一个法向量为
的一个法向量为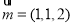 ,
,
取平面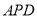 的一个法向量为
的一个法向量为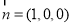 ,∴
,∴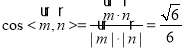 ,∴二面角
,∴二面角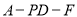 的平面角的余弦值为
的平面角的余弦值为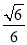 .
.

考点:1.空间直角坐标系的建立;2.二面角与法向量的运用.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 ,且
,且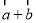 与
与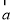 共线,那么
共线,那么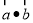 的值为( )
的值为( ) 的抛物线的标准方程是( )
的抛物线的标准方程是( )
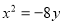
 或
或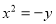
 或
或 对定义域
对定义域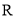 内的任意
内的任意 都有
都有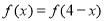 ,且当
,且当 时,其导函数
时,其导函数
 ,若
,若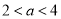 ,则( )
,则( )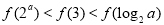
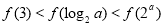

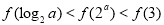
 是( )
是( )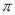 的奇函数
的奇函数 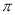 的偶函数
的偶函数 的奇函数
的奇函数  的外接圆半径为
的外接圆半径为 ,圆心为
,圆心为 ,且
,且 ,则
,则 的值为 .
的值为 . ,
,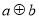 的运算原理如图所示,设
的运算原理如图所示,设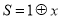 ,
,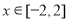 ,则输出的
,则输出的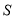 的最大值与最小值的差为( )
的最大值与最小值的差为( )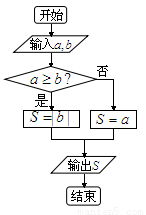
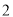 B.
B.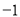 C.
C.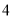 D.
D.
 的各项均为正数,且
的各项均为正数,且 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 ,则
,则  中元素的个数为_______.
中元素的个数为_______.