题目内容

已知△ABC的外接圆半径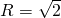 $数学公式$ ，a、b、C分别为∠A、∠B、∠C的对边，向量 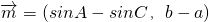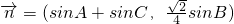$数学公式$ ， $数学公式$ ，且 $数学公式$ ．
（1）求∠C的大小；
（2）求△ABC面积的最大值．

解：（1）∵ $\text{[math]}$
∴ $\text{[math]}$
且 $\text{[math]}$ ，由正弦定理得： $\text{[math]}$
化简得：c²=a²+b²-ab
由余弦定理：c²=a²+b²-2abcosC∴ $\text{[math]}$ ，
∵0＜C＜π，∴ $\text{[math]}$
（2）∵a²+b²-ab=c²=（2RsinC）²=6，
∴6=a²+b²-ab≥2ab-ab=ab（当且仅当a=b时取“=”），
$\text{[math]}$
所以， $\text{[math]}$ ．
分析：（1）由 $\text{[math]}$ ，推出 $\text{[math]}$ ，利用坐标表示化简表达式，结合余弦定理求角C；
（2）利用（1）中c²=a²+b²-ab，应用正弦定理和基本不等式，求三角形ABC的面积S的最大值．
点评：本题考查数量积判断两个平面向量的垂直关系，正弦定理，余弦定理的应用，考查学生分析问题解决问题的能力，是中档题．

练习册系列答案

寒假作业南方日报出版社系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

相关题目

已知△ABC的外接圆的圆心O，BC＞CA＞AB，则

的大小关系为

已知△ABC的外接圆的半径为

，内角A，B，C的对边分别为a，b，c，又向量

=(sinA-sinC，b-a)，

，
（I）求角C；
（II）求三角形ABC的面积S的最大值．

已知△ABC的外接圆半径R为6，面积为S，a、b、c分别是角A、B、C的对边设S=a2-(b-c)2，sinB+sinC=

．
（I）求sinA的值；
（II）求△ABC面积的最大值．

已知△ABC的外接圆半径为1，角A，B，C的对边分别为a，b，c．向量

=(a，4cosB)，

=(cosA，b)满足

．
（1）求sinA+sinB的取值范围；
（2）若A∈(0，

)，且实数x满足abx=a-b，试确定x的取值范围．

已知△ABC的外接圆圆心为O，BC＞CA＞AB．则（　　）