题目内容
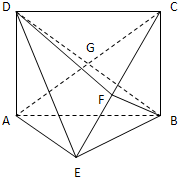 如图,E为矩形ABCD所在平面外一点,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC∩BD=G.
如图,E为矩形ABCD所在平面外一点,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC∩BD=G.
(1)求证:AE⊥平面BCE;
(2)求三棱锥C-BGF的体积.
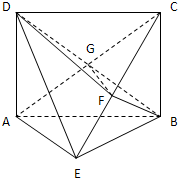 解:(1)证明:∵AD⊥平面ABE,AD∥BC.
解:(1)证明:∵AD⊥平面ABE,AD∥BC.∴BC⊥平面ABE,则AE⊥BC.…(3分)
又∵BF⊥平面ACE,则AE⊥BF.…(5分)
又BC∩BF=B,∴AE⊥平面BCE.…(7分)
(2)由题意,得G是AC的中点,连FG,
∵BF⊥平面ACE,则CE⊥BF.
而BC=BE,∴F是EC的中点…(9分)
∴AE∥FG,且
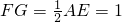 .
.而AE⊥平面BCE,∴FG⊥平面BCF.…(11分)
∴
 .
.∴
 .
.∴
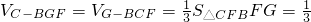 .…(13分)
.…(13分)分析:(1)通过AD⊥平面ABE,得到AE⊥BC,证明AE⊥BF.然后证明AE⊥平面BCE;
(2)得G是AC的中点,连FG,推出CE⊥BF.通过F是EC的中点,然后证明FG⊥平面BCF求出S△CFB.然后求出体积.
点评:本题考查直线与平面垂直的判定定理的应用,几何体的体积的求法,考查计算能力.

练习册系列答案
相关题目
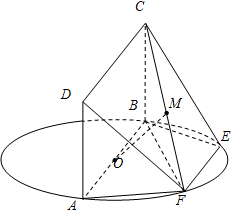 (2012•湘潭三模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD的边BC垂直于圆O所在的平面,且AB=2,AD=EF=1.
(2012•湘潭三模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD的边BC垂直于圆O所在的平面,且AB=2,AD=EF=1. (2012•衡阳模拟)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD的边BC垂直于圆O所在的平面,且AB=2,AD=EF=1.
(2012•衡阳模拟)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD的边BC垂直于圆O所在的平面,且AB=2,AD=EF=1.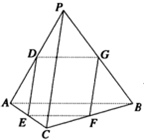 如图,在四面体P-ABC中,PC⊥AB,PA⊥BC,点D、E、F、G分别是棱AP、AC、CB、BP的中点;
如图,在四面体P-ABC中,PC⊥AB,PA⊥BC,点D、E、F、G分别是棱AP、AC、CB、BP的中点;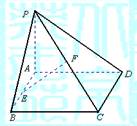

 BC,FO
BC,FO

 ,点E是斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为
,点E是斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为 ,
,