题目内容
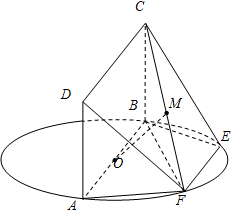 (2012•湘潭三模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD的边BC垂直于圆O所在的平面,且AB=2,AD=EF=1.
(2012•湘潭三模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD的边BC垂直于圆O所在的平面,且AB=2,AD=EF=1.(Ⅰ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅱ)求三棱锥F-ABC的体积VF-ABC.
分析:(I)设DF的中点为N,连接MN、AN,利用三角形中位线定理并结合矩形ABCD的性质,得四边形MNAO为平行四边形,从而OM∥AN,可得OM∥平面DAF;
(II)在圆O中根据平面几何知识,得等腰梯形ABEF中,AF=BE=1且BF=
,算出△ABF的面积,根据BC⊥平面ABEF,结合锥体体积公式可算出三棱锥F-ABC的体积VF-ABC.
(II)在圆O中根据平面几何知识,得等腰梯形ABEF中,AF=BE=1且BF=
| 3 |
解答:解:(Ⅰ)设DF的中点为N,连接MN、AN,则
∵△CDF中,M、N分别为CF、DF的中点
∴MN∥CD且MN=
CD,
又∵矩形ABCD中,AO∥CD且AO=
CD,
∴MN∥AO且MN=AO,得四边形MNAO为平行四边形 …(2分)
∴OM∥AN,又AN?平面DAF,OM?平面DAF…(4分)
∴OM∥平面DAF…(6分)
(Ⅱ)∵圆O中,EF∥AB,
∴AF=BE,四边形ABEF是等腰梯形
∵AB=2,AF⊥BF,EF=1
∴AF=BE=1,BF=
,…(8分)
因此,S△ABF=
AF×BF=
…(10分)
又∵CB⊥平面ABEF
∴VF-ABC=VC-ABF=
CB•S△ABF=
…(12分)

∵△CDF中,M、N分别为CF、DF的中点
∴MN∥CD且MN=
| 1 |
| 2 |
又∵矩形ABCD中,AO∥CD且AO=
| 1 |
| 2 |
∴MN∥AO且MN=AO,得四边形MNAO为平行四边形 …(2分)
∴OM∥AN,又AN?平面DAF,OM?平面DAF…(4分)
∴OM∥平面DAF…(6分)
(Ⅱ)∵圆O中,EF∥AB,
∴AF=BE,四边形ABEF是等腰梯形
∵AB=2,AF⊥BF,EF=1
∴AF=BE=1,BF=
| 3 |
因此,S△ABF=
| 1 |
| 2 |
| ||
| 2 |
又∵CB⊥平面ABEF
∴VF-ABC=VC-ABF=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
点评:本题在特殊的四棱锥中证明线面平行,并求三棱锥的体积,着重考查了空间的线面垂直、线面平行的判定与性质,锥体体积的求法等知识,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目